• 4.3 左角落分析器

    4.3 左角落分析器

    递归下降分析器的问题之一是当它遇到一个左递归产生式时，会进入无限循环。这是因为它盲目应用文法产生式而不考虑实际输入的句子。左角落分析器是我们已经看到的自下而上与自上而下方法的混合体。

    语法grammar1允许我们对 John saw Mary 生成下面的分析：

    1. >>> text = ['I', 'shot', 'an', 'elephant', 'in', 'my', 'pajamas']
    2. >>> groucho_grammar.productions(rhs=text[1])
    3. [V -> 'shot']

    对于我们的 WFST，我们用 Python 中的列表的咧表创建一个(n-1) × (n-1)的矩阵，在4.4中的函数init_wfst()中用每个标识符的词汇类型初始化它。我们还定义一个实用的函数display()来为我们精美的输出 WFST。正如预期的那样，V在(1, 2)单元中。

    1. def init_wfst(tokens, grammar):
    2.     numtokens = len(tokens)
    3.     wfst = [[None for i in range(numtokens+1)] for j in range(numtokens+1)]
    4.     for i in range(numtokens):
    5.         productions = grammar.productions(rhs=tokens[i])
    6.         wfst[i][i+1] = productions[0].lhs()
    7.     return wfst
    9. def complete_wfst(wfst, tokens, grammar, trace=False):
    10.     index = dict((p.rhs(), p.lhs()) for p in grammar.productions())
    11.     numtokens = len(tokens)
    12.     for span in range(2, numtokens+1):
    13.         for start in range(numtokens+1-span):
    14.             end = start + span
    15.             for mid in range(start+1, end):
    16.                 nt1, nt2 = wfst[start][mid], wfst[mid][end]
    17.                 if nt1 and nt2 and (nt1,nt2) in index:
    18.                     wfst[start][end] = index[(nt1,nt2)]
    19.                     if trace:
    20.                         print("[%s] %3s [%s] %3s [%s] ==> [%s] %3s [%s]" % \
    21.                         (start, nt1, mid, nt2, end, start, index[(nt1,nt2)], end))
    22.     return wfst
    24. def display(wfst, tokens):
    25.     print('\nWFST ' + ' '.join(("%-4d" % i) for i in range(1, len(wfst))))
    26.     for i in range(len(wfst)-1):
    27.         print("%d   " % i, end=" ")
    28.         for j in range(1, len(wfst)):
    29.             print("%-4s" % (wfst[i][j] or '.'), end=" ")
    30.         print()
    31. >>> tokens = "I shot an elephant in my pajamas".split()
    32. >>> wfst0 = init_wfst(tokens, groucho_grammar)
    33. >>> display(wfst0, tokens)
    34. WFST 1    2    3    4    5    6    7
    35. 0    NP   .    .    .    .    .    .
    36. 1    .    V    .    .    .    .    .
    37. 2    .    .    Det  .    .    .    .
    38. 3    .    .    .    N    .    .    .
    39. 4    .    .    .    .    P    .    .
    40. 5    .    .    .    .    .    Det  .
    41. 6    .    .    .    .    .    .    N
    42. >>> wfst1 = complete_wfst(wfst0, tokens, groucho_grammar)
    43. >>> display(wfst1, tokens)
    44. WFST 1    2    3    4    5    6    7
    45. 0    NP   .    .    S    .    .    S
    46. 1    .    V    .    VP   .    .    VP
    47. 2    .    .    Det  NP   .    .    .
    48. 3    .    .    .    N    .    .    .
    49. 4    .    .    .    .    P    .    PP
    50. 5    .    .    .    .    .    Det  NP
    51. 6    .    .    .    .    .    .    N

    回到我们的表格表示，假设对于词 an 我们有Det在(2, 3)单元，对以词 elephant 有N在(3, 4)单元，对于 an elephant 我们应该在(2, 4)放入什么？我们需要找到一个形如 A → Det N的产生式。查询了文法，我们知道我们可以输入(0, 2)单元的NP。

    更一般的，我们可以在(i, j)输入 A，如果有一个产生式 A → B C，并且我们在(i, k)中找到非终结符 B，在(k, j)中找到非终结符 C。4.4中的程序使用此规则完成 WFST。通过调用函数complete_wfst()时设置 trace为True，我们看到了显示 WFST 正在被创建的跟踪输出：

    1. >>> wfst1 = complete_wfst(wfst0, tokens, groucho_grammar, trace=True)
    2. [2] Det [3]   N [4] ==> [2]  NP [4]
    3. [5] Det [6]   N [7] ==> [5]  NP [7]
    4. [1]   V [2]  NP [4] ==> [1]  VP [4]
    5. [4]   P [5]  NP [7] ==> [4]  PP [7]
    6. [0]  NP [1]  VP [4] ==> [0]   S [4]
    7. [1]  VP [4]  PP [7] ==> [1]  VP [7]
    8. [0]  NP [1]  VP [7] ==> [0]   S [7]

    例如，由于我们在wfst[2][3]找到Det，在wfst[3][4]找到N，我们可以添加NP到wfst[2][4]。

    注意

    为了帮助我们更简便地通过产生式的右侧检索产生式，我们为语法创建一个索引。这是空间-时间权衡的一个例子：我们对语法做反向查找，每次我们想要通过右侧查找产生式时不必遍历整个产生式列表。

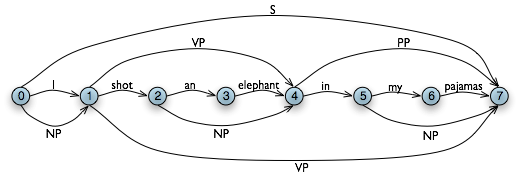
    Images/chart_positions2.png

    图 4.5：图数据结构：图中额外的边表示非终结符。

    我们得出结论，只要我们已经在(0, 7)单元构建了一个S节点，表明我们已经找到了一个涵盖了整个输入的句子，我们就为整个输入字符串找到了一个解析。最后的 WFST 状态如4.5所示。

    请注意，在这里我们没有使用任何内置的分析函数。我们已经从零开始实现了一个完整的初级图表分析器！

    WFST 有几个缺点。首先，正如你可以看到的，WFST 本身不是一个分析树，所以该技术严格地说是认识到一个句子被一个语法承认，而不是分析它。其次，它要求每个非词汇语法生产式是二元的。虽然可以将任意的 CFG 转换为这种形式，我们宁愿使用这种方法时没有这样的规定。第三，作为一个自下而上的语法，它潜在的存在浪费，它会在不符合文法的地方提出成分。

    最后，WFST 并不能表示句子中的结构歧义（如两个动词短语的读取）。(1, 7)单元中的VP实际上被输入了两次，一次是读取V NP，一次是读取VP PP 。这是不同的假设，第二个会覆盖第一个（虽然如此，这并不重要，因为左侧是相同的。）图表分析器使用稍微更丰富的数据结构和一些有趣的算法来解决这些问题（详细情况参见本章末尾的进一步阅读一节）。

    注意

    轮到你来：尝试交互式图表分析器应用程序nltk.app.chartparser()。