数值微分

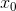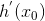从数值上说，最简单的方案是去计算导数的近似值。回忆h(x)在 x_0 的导数 h^{'}(x_0)，是该函数在该点处的斜率，或者更准确如公式 D-2 所示。

E_D-2

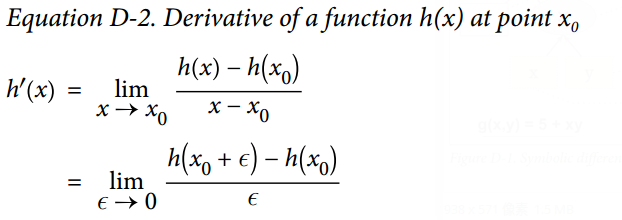
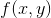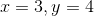因此如果我们想要计算 f(x,y) 关于x，在 x=3, y=4 处的导数，我们可以简单计算 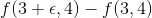f(3+\epsilon, 4) - f(3, 4) 的值，将这个结果除以 \epsilon，且 \epsilon 去很小的值。这个过程正是如下的代码所要干的。

  1. def f(x, y):
  2.     return x**2*y + y + 2
  4. def derivative(f, x, y, x_eps, y_eps):
  5.     return (f(x + x_eps, y + y_eps) - f(x, y)) / (x_eps + y_eps)
  7. df_dx = derivative(f, 3, 4, 0.00001, 0)
  8. df_dy = derivative(f, 3, 4, 0, 0.00001)

不幸的是，偏导的结果并不准确（并且可能在求解复杂函数时更糟糕）。上述正确答案分别是 24 和 10 ，但我们得到的是：

  1. >>> print(df_dx)
  2. 24.000039999805264
  3. >>> print(df_dy)
  4. 10.000000000331966

注意到为了计算两个偏导数， 我们不得不调用f()至少三次（在上述代码里我们调用了四次，但可以优化）。如果存在 1000 个参数，我们将会调用f()至少 1001 次。当处理大的神经网络时，这样的操作很没有效率。

然而，数值微分实现起来如此简单，以至于它是检查其他方法正确性的优秀工具。例如，如果它的结果与您手动计算的导数不同，那么你的导数可能包含错误。