逻辑回归
正如我们在第1章中讨论的那样,一些回归算法也可以用于分类(反之亦然)。 Logistic 回归(也称为 Logit 回归)通常用于估计一个实例属于某个特定类别的概率(例如,这电子邮件是垃圾邮件的概率是多少?)。 如果估计的概率大于 50%,那么模型预测这个实例属于当前类(称为正类,标记为“1”),反之预测它不属于当前类(即它属于负类 ,标记为“0”)。 这样便成为了一个二元分类器。
概率估计
那么它是怎样工作的? 就像线性回归模型一样,Logistic 回归模型计算输入特征的加权和(加上偏差项),但它不像线性回归模型那样直接输出结果,而是把结果输入logistic()函数进行二次加工后进行输出(详见公式 4-13)。
公式 4-13:逻辑回归模型的概率估计(向量形式)
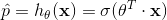
Logistic 函数(也称为 logit),用 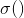 表示,其是一个 sigmoid 函数(图像呈 S 型),它的输出是一个介于 0 和 1 之间的数字。其定义如公式 4-14 和图 4-21 所示。
表示,其是一个 sigmoid 函数(图像呈 S 型),它的输出是一个介于 0 和 1 之间的数字。其定义如公式 4-14 和图 4-21 所示。
公式 4-14:逻辑函数
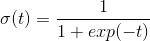
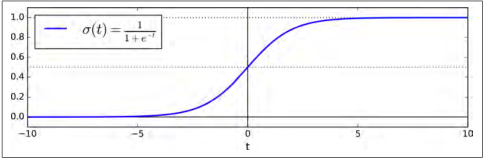
图4-21:逻辑函数
一旦 Logistic 回归模型估计得到了 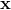 属于正类的概率
属于正类的概率 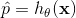 ,那它很容易得到预测结果
,那它很容易得到预测结果 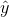 (见公式 4-15)。
(见公式 4-15)。
公式 4-15:逻辑回归预测模型
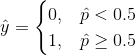
注意当 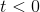 时
时 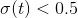 ,当
,当 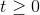 时
时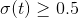 ,因此当
,因此当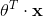 是正数的话,逻辑回归模型输出 1,如果它是负数的话,则输出 0。
是正数的话,逻辑回归模型输出 1,如果它是负数的话,则输出 0。
训练和损失函数
好,现在你知道了 Logistic 回归模型如何估计概率并进行预测。 但是它是如何训练的? 训练的目的是设置参数向量 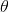 ,使得正例(
,使得正例(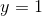 )概率增大,负例(
)概率增大,负例(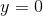 )的概率减小,其通过在单个训练实例
)的概率减小,其通过在单个训练实例 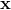 的损失函数来实现(公式 4-16)。
的损失函数来实现(公式 4-16)。
公式 4-16:单个样本的损失函数
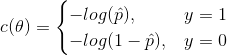
这个损失函数是合理的,因为当 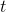 接近 0 时,
接近 0 时,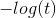 变得非常大,所以如果模型估计一个正例概率接近于 0,那么损失函数将会很大,同时如果模型估计一个负例的概率接近 1,那么损失函数同样会很大。 另一方面,当
变得非常大,所以如果模型估计一个正例概率接近于 0,那么损失函数将会很大,同时如果模型估计一个负例的概率接近 1,那么损失函数同样会很大。 另一方面,当 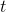 接近于 1 时,
接近于 1 时,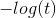 接近 0,所以如果模型估计一个正例概率接近于 0,那么损失函数接近于 0,同时如果模型估计一个负例的概率接近 0,那么损失函数同样会接近于 0, 这正是我们想的。
接近 0,所以如果模型估计一个正例概率接近于 0,那么损失函数接近于 0,同时如果模型估计一个负例的概率接近 0,那么损失函数同样会接近于 0, 这正是我们想的。
整个训练集的损失函数只是所有训练实例的平均值。可以用一个表达式(你可以很容易证明)来统一表示,称为对数损失,如公式 4-17 所示。
公式 4-17:逻辑回归的损失函数(对数损失)
![J(\theta)=-\frac{1}{m}\sum\limits_{i=1}^m\left[y^{(i)}log\left(\hat{p}^{(i)}\right)+\left(1-y^{(i)}\right)log\left(1-\hat{p}^{(i)}\right)\right]](/uploads/projects/1762/67060.gif)
但是这个损失函数对于求解最小化损失函数的 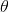 是没有公式解的(没有等价的正态方程)。 但好消息是,这个损失函数是凸的,所以梯度下降(或任何其他优化算法)一定能够找到全局最小值(如果学习速率不是太大,并且你等待足够长的时间)。公式 4-18 给出了损失函数关于第
是没有公式解的(没有等价的正态方程)。 但好消息是,这个损失函数是凸的,所以梯度下降(或任何其他优化算法)一定能够找到全局最小值(如果学习速率不是太大,并且你等待足够长的时间)。公式 4-18 给出了损失函数关于第 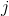 个模型参数
个模型参数 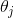 的偏导数。
的偏导数。
公式 4-18:逻辑回归损失函数的偏导数
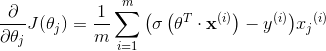
这个公式看起来非常像公式 4-5:首先计算每个样本的预测误差,然后误差项乘以第 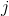 项特征值,最后求出所有训练样本的平均值。 一旦你有了包含所有的偏导数的梯度向量,你便可以在梯度向量上使用批量梯度下降算法。 也就是说:你已经知道如何训练 Logistic 回归模型。 对于随机梯度下降,你当然只需要每一次使用一个实例,对于小批量梯度下降,你将每一次使用一个小型实例集。
项特征值,最后求出所有训练样本的平均值。 一旦你有了包含所有的偏导数的梯度向量,你便可以在梯度向量上使用批量梯度下降算法。 也就是说:你已经知道如何训练 Logistic 回归模型。 对于随机梯度下降,你当然只需要每一次使用一个实例,对于小批量梯度下降,你将每一次使用一个小型实例集。
决策边界
我们使用鸢尾花数据集来分析 Logistic 回归。 这是一个著名的数据集,其中包含 150 朵三种不同的鸢尾花的萼片和花瓣的长度和宽度。这三种鸢尾花为:Setosa,Versicolor,Virginica(如图 4-22)。

图4-22:三种不同的鸢尾花
让我们尝试建立一个分类器,仅仅使用花瓣的宽度特征来识别 Virginica,首先让我们加载数据:
>>> from sklearn import datasets>>> iris = datasets.load_iris()>>> list(iris.keys())['data', 'target_names', 'feature_names', 'target', 'DESCR']>>> X = iris["data"][:, 3:] # petal width>>> y = (iris["target"] == 2).astype(np.int)
接下来,我们训练一个逻辑回归模型:
from sklearn.linear_model import LogisticRegressionlog_reg = LogisticRegression()log_reg.fit(X, y)
我们来看看模型估计的花瓣宽度从 0 到 3 厘米的概率估计(如图 4-23):
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)y_proba = log_reg.predict_proba(X_new)plt.plot(X_new, y_proba[:, 1], "g-", label="Iris-Virginica")plt.plot(X_new, y_proba[:, 0], "b--", label="Not Iris-Virginica"
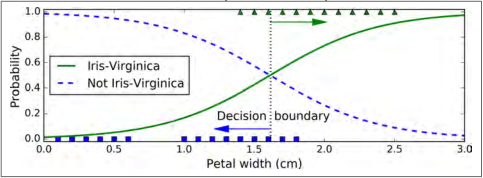
图 4-23:概率估计和决策边界
Virginica 花的花瓣宽度(用三角形表示)在 1.4 厘米到 2.5 厘米之间,而其他种类的花(由正方形表示)通常具有较小的花瓣宽度,范围从 0.1 厘米到 1.8 厘米。注意,它们之间会有一些重叠。在大约 2 厘米以上时,分类器非常肯定这朵花是Virginica花(分类器此时输出一个非常高的概率值),而在1厘米以下时,它非常肯定这朵花不是 Virginica 花(不是 Virginica 花有非常高的概率)。在这两个极端之间,分类器是不确定的。但是,如果你使用它进行预测(使用predict()方法而不是predict_proba()方法),它将返回一个最可能的结果。因此,在 1.6 厘米左右存在一个决策边界,这时两类情况出现的概率都等于 50%:如果花瓣宽度大于 1.6 厘米,则分类器将预测该花是 Virginica,否则预测它不是(即使它有可能错了):
>>> log_reg.predict([[1.7], [1.5]])array([1, 0])
图 4-24 表示相同的数据集,但是这次使用了两个特征进行判断:花瓣的宽度和长度。 一旦训练完毕,Logistic 回归分类器就可以根据这两个特征来估计一朵花是 Virginica 的可能性。 虚线表示这时两类情况出现的概率都等于 50%:这是模型的决策边界。 请注意,它是一个线性边界。每条平行线都代表一个分类标准下的两两个不同类的概率,从 15%(左下角)到 90%(右上角)。越过右上角分界线的点都有超过 90% 的概率是 Virginica 花。
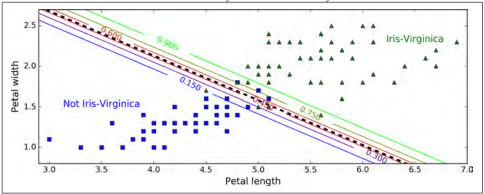
图 4-24:线性决策边界
就像其他线性模型,逻辑回归模型也可以 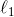 或者
或者 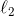 惩罚使用进行正则化。Scikit-Learn 默认添加了
惩罚使用进行正则化。Scikit-Learn 默认添加了 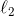 惩罚。
惩罚。
注意
在 Scikit-Learn 的
LogisticRegression模型中控制正则化强度的超参数不是(与其他线性模型一样),而是它的逆:
。
的值越大,模型正则化强度越低。
Softmax 回归
Logistic 回归模型可以直接推广到支持多类别分类,不必组合和训练多个二分类器(如第 3 章所述), 其称为 Softmax 回归或多类别 Logistic 回归。
这个想法很简单:当给定一个实例 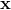 时,Softmax 回归模型首先计算
时,Softmax 回归模型首先计算 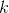 类的分数
类的分数 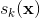 ,然后将分数应用在
,然后将分数应用在Softmax函数(也称为归一化指数)上,估计出每类的概率。 计算 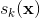 的公式看起来很熟悉,因为它就像线性回归预测的公式一样(见公式 4-19)。
的公式看起来很熟悉,因为它就像线性回归预测的公式一样(见公式 4-19)。
公式 4-19:k类的 Softmax 得分
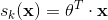
注意,每个类都有自己独一无二的参数向量 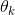 。 所有这些向量通常作为行放在参数矩阵
。 所有这些向量通常作为行放在参数矩阵 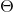 中。
中。
一旦你计算了样本 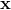 的每一类的得分,你便可以通过
的每一类的得分,你便可以通过Softmax函数(公式 4-20)估计出样本属于第 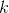 类的概率
类的概率 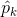 :通过计算
:通过计算  的
的 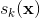 次方,然后对它们进行归一化(除以所有分子的总和)。
次方,然后对它们进行归一化(除以所有分子的总和)。
公式 4-20:Softmax 函数
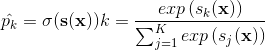
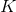 表示有多少类
表示有多少类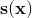 表示包含样本
表示包含样本 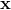 每一类得分的向量
每一类得分的向量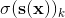 表示给定每一类分数之后,实例
表示给定每一类分数之后,实例 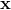 属于第
属于第 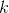 类的概率
类的概率
和 Logistic 回归分类器一样,Softmax 回归分类器将估计概率最高(它只是得分最高的类)的那类作为预测结果,如公式 4-21 所示。
公式 4-21:Softmax 回归模型分类器预测结果
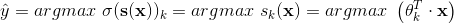
argmax运算返回一个函数取到最大值的变量值。 在这个等式,它返回使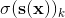 最大时的
最大时的 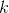 的值
的值
注意
Softmax 回归分类器一次只能预测一个类(即它是多类的,但不是多输出的),因此它只能用于判断互斥的类别,如不同类型的植物。 你不能用它来识别一张照片中的多个人。
现在我们知道这个模型如何估计概率并进行预测,接下来将介绍如何训练。我们的目标是建立一个模型在目标类别上有着较高的概率(因此其他类别的概率较低),最小化公式 4-22 可以达到这个目标,其表示了当前模型的损失函数,称为交叉熵,当模型对目标类得出了一个较低的概率,其会惩罚这个模型。 交叉熵通常用于衡量待测类别与目标类别的匹配程度(我们将在后面的章节中多次使用它)
公式 4-22:交叉熵
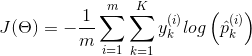
- 如果对于第
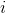 个实例的目标类是
个实例的目标类是 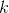 ,那么
,那么 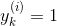 ,反之
,反之 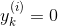 。
。
可以看出,当只有两个类(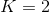 )时,此损失函数等同于 Logistic 回归的损失函数(对数损失;请参阅公式 4-17)。
)时,此损失函数等同于 Logistic 回归的损失函数(对数损失;请参阅公式 4-17)。
交叉熵
交叉熵源于信息论。假设你想要高效地传输每天的天气信息。如果有八个选项(晴天,雨天等),则可以使用3位对每个选项进行编码,因为
。但是,如果你认为几乎每天都是晴天,更高效的编码“晴天”的方式是:只用一位(0)。剩下的七项使用四位(从 1 开始)。交叉熵度量每个选项实际发送的平均比特数。 如果你对天气的假设是完美的,交叉熵就等于天气本身的熵(即其内部的不确定性)。 但是,如果你的假设是错误的(例如,如果经常下雨)交叉熵将会更大,称为 Kullback-Leibler 散度(KL 散度)。
两个概率分布
和
之间的交叉熵定义为:
(分布至少是离散的)
这个损失函数关于 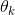 的梯度向量为公式 4-23:
的梯度向量为公式 4-23:
公式 4-23:k类交叉熵的梯度向量
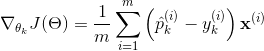
现在你可以计算每一类的梯度向量,然后使用梯度下降(或者其他的优化算法)找到使得损失函数达到最小值的参数矩阵 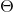 。
。
让我们使用 Softmax 回归对三种鸢尾花进行分类。当你使用LogisticRregression对模型进行训练时,Scikit Learn 默认使用的是一对多模型,但是你可以设置multi_class参数为“multinomial”来把它改变为 Softmax 回归。你还必须指定一个支持 Softmax 回归的求解器,例如“lbfgs”求解器(有关更多详细信息,请参阅 Scikit-Learn 的文档)。其默认使用 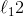 正则化,你可以使用超参数
正则化,你可以使用超参数 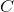 控制它。
控制它。
X = iris["data"][:, (2, 3)] # petal length, petal widthy = iris["target"]softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10)softmax_reg.fit(X, y)
所以下次你发现一个花瓣长为 5 厘米,宽为 2 厘米的鸢尾花时,你可以问你的模型你它是哪一类鸢尾花,它会回答 94.2% 是 Virginica 花(第二类),或者 5.8% 是其他鸢尾花。
>>> softmax_reg.predict([[5, 2]])array([2])>>> softmax_reg.predict_proba([[5, 2]])array([[ 6.33134078e-07, 5.75276067e-02, 9.42471760e-01]])是
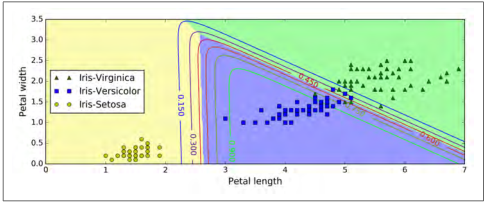
图 4-25:Softmax 回归的决策边界
图 4-25 用不同背景色表示了结果的决策边界。注意,任何两个类之间的决策边界是线性的。 该图的曲线表示 Versicolor 类的概率(例如,用 0.450 标记的曲线表示 45% 的概率边界)。注意模型也可以预测一个概率低于 50% 的类。 例如,在所有决策边界相遇的地方,所有类的估计概率相等,分别为 33%。
