- 循环神经网络(RNN)
循环神经网络(RNN)
循环神经网络(Recurrent Neural Network, RNN)是一种适宜于处理序列数据的神经网络,被广泛用于语言模型、文本生成、机器翻译等。
基础知识和原理
Recurrent Neural Networks Tutorial, Part 1 – Introduction to RNNs
台湾大学李宏毅教授的《机器学习》课程的 Recurrent Neural Network (part 1)Recurrent Neural Network (part 2) 两部分。
LSTM 原理:Understanding LSTM Networks
RNN 序列生成:[Graves2013]
这里,我们使用 RNN 来进行尼采风格文本的自动生成。 5
这个任务的本质其实预测一段英文文本的接续字母的概率分布。比如,我们有以下句子:
- I am a studen
这个句子(序列)一共有 13 个字符(包含空格)。当我们阅读到这个由 13 个字符组成的序列后,根据我们的经验,我们可以预测出下一个字符很大概率是 “t”。我们希望建立这样一个模型,逐个输入一段长为 seq_length 的序列,输出这些序列接续的下一个字符的概率分布。我们从下一个字符的概率分布中采样作为预测值,然后滚雪球式地生成下两个字符,下三个字符等等,即可完成文本的生成任务。
首先,还是实现一个简单的 DataLoader 类来读取文本,并以字符为单位进行编码。设字符种类数为 num_chars ,则每种字符赋予一个 0 到 num_chars - 1 之间的唯一整数编号 i。
- class DataLoader():
- def __init__(self):
- path = tf.keras.utils.get_file('nietzsche.txt',
- origin='https://s3.amazonaws.com/text-datasets/nietzsche.txt')
- with open(path, encoding='utf-8') as f:
- self.raw_text = f.read().lower()
- self.chars = sorted(list(set(self.raw_text)))
- self.char_indices = dict((c, i) for i, c in enumerate(self.chars))
- self.indices_char = dict((i, c) for i, c in enumerate(self.chars))
- self.text = [self.char_indices[c] for c in self.raw_text]
- def get_batch(self, seq_length, batch_size):
- seq = []
- next_char = []
- for i in range(batch_size):
- index = np.random.randint(0, len(self.text) - seq_length)
- seq.append(self.text[index:index+seq_length])
- next_char.append(self.text[index+seq_length])
- return np.array(seq), np.array(next_char) # [batch_size, seq_length], [num_batch]
接下来进行模型的实现。在 init 方法中我们实例化一个常用的 LSTMCell 单元,以及一个线性变换用的全连接层,我们首先对序列进行“One Hot”操作,即将序列中的每个字符的编码 i 均变换为一个 num_char 维向量,其第 i 位为 1,其余均为 0。变换后的序列张量形状为 [seq_length, num_chars] 。然后,我们初始化 RNN 单元的状态,存入变量 state 中。接下来,将序列从头到尾依次送入 RNN 单元,即在 t 时刻,将上一个时刻 t-1 的 RNN 单元状态 state 和序列的第 t 个元素 inputs[t, :] 送入 RNN 单元,得到当前时刻的输出 output 和 RNN 单元状态。取 RNN 单元最后一次的输出,通过全连接层变换到 num_chars 维,即作为模型的输出。
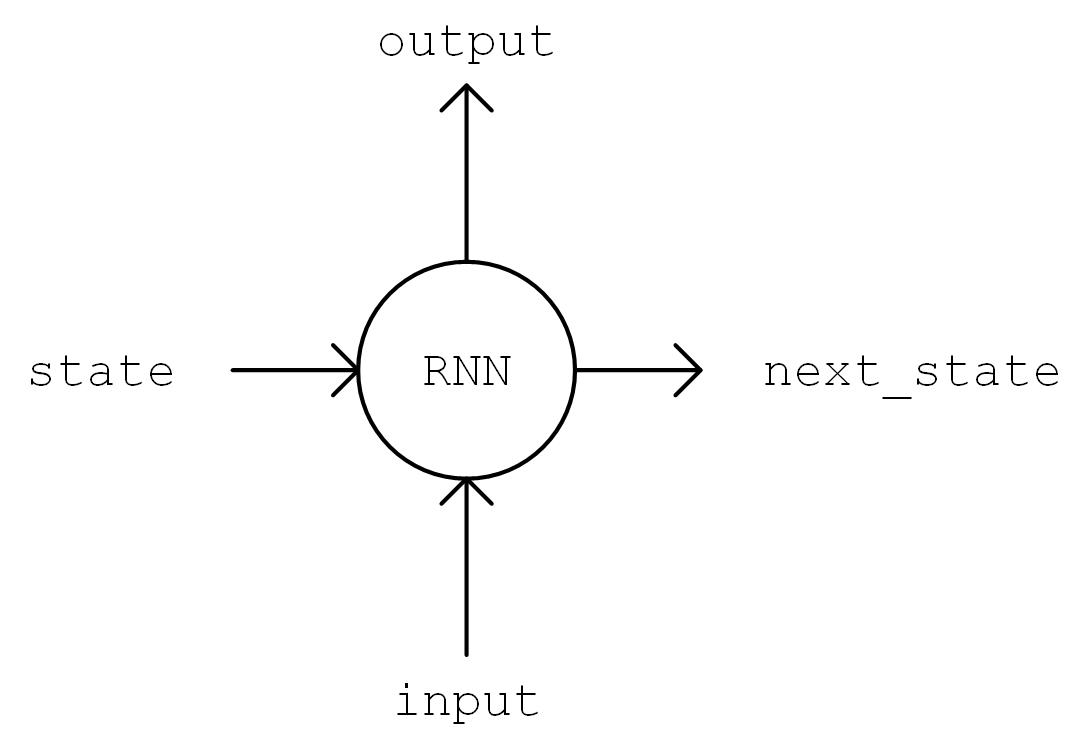
output, state = self.cell(inputs[:, t, :], state) 图示
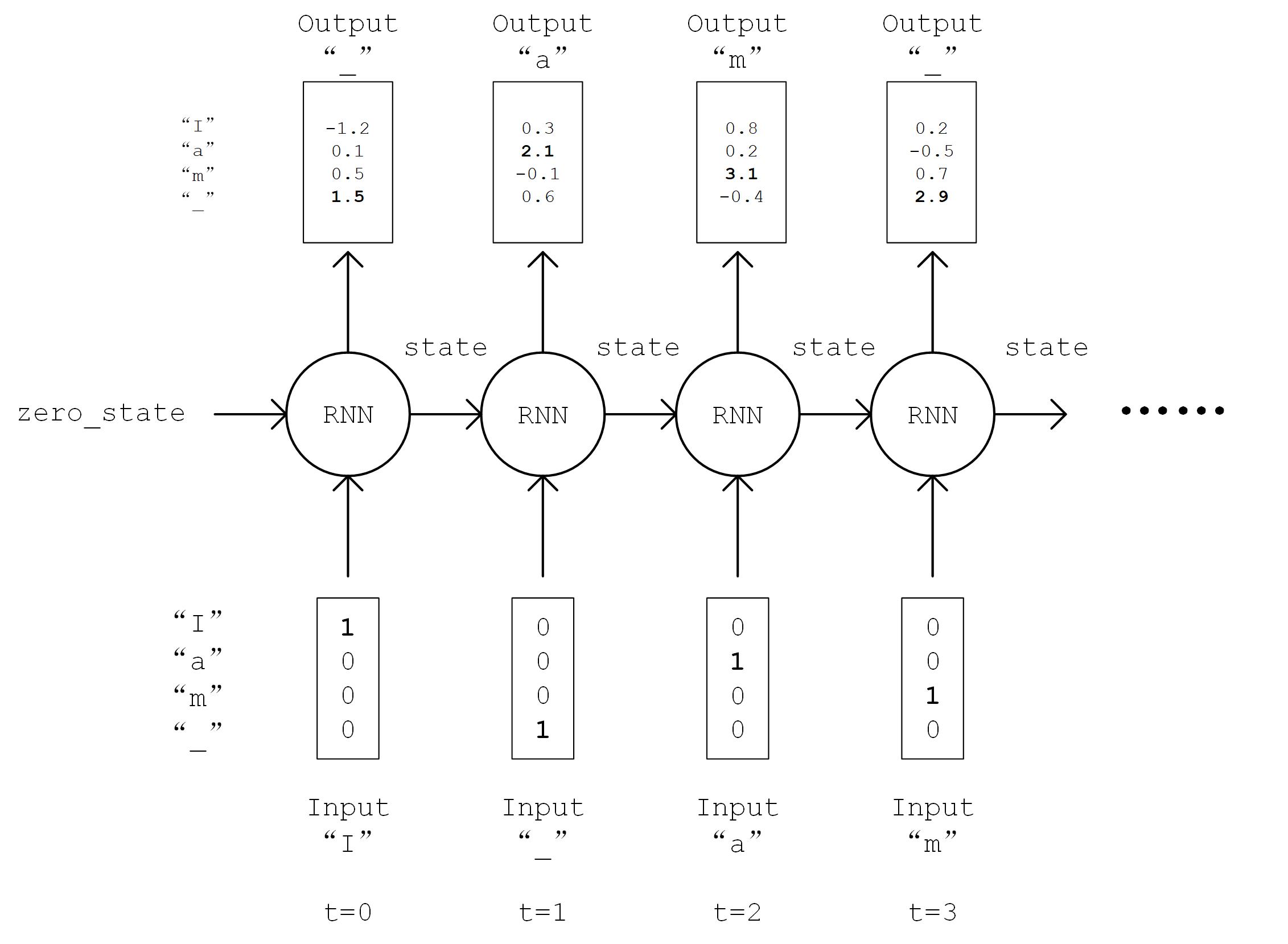 RNN 流程图示
RNN 流程图示
具体实现如下:
- class RNN(tf.keras.Model):
- def __init__(self, num_chars, batch_size, seq_length):
- super().__init__()
- self.num_chars = num_chars
- self.seq_length = seq_length
- self.batch_size = batch_size
- self.cell = tf.keras.layers.LSTMCell(units=256)
- self.dense = tf.keras.layers.Dense(units=self.num_chars)
- def call(self, inputs, from_logits=False):
- inputs = tf.one_hot(inputs, depth=self.num_chars) # [batch_size, seq_length, num_chars]
- state = self.cell.get_initial_state(batch_size=self.batch_size, dtype=tf.float32)
- for t in range(self.seq_length):
- output, state = self.cell(inputs[:, t, :], state)
- logits = self.dense(output)
- if from_logits:
- return logits
- else:
- return tf.nn.softmax(logits)
定义一些模型超参数:
- num_batches = 1000
- seq_length = 40
- batch_size = 50
- learning_rate = 1e-3
训练过程与前节基本一致,在此复述:
从
DataLoader中随机取一批训练数据;将这批数据送入模型,计算出模型的预测值;
将模型预测值与真实值进行比较,计算损失函数(loss);
计算损失函数关于模型变量的导数;
使用优化器更新模型参数以最小化损失函数。
- data_loader = DataLoader()
- model = RNN(num_chars=len(data_loader.chars), batch_size=batch_size, seq_length=seq_length)
- optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate)
- for batch_index in range(num_batches):
- X, y = data_loader.get_batch(seq_length, batch_size)
- with tf.GradientTape() as tape:
- y_pred = model(X)
- loss = tf.keras.losses.sparse_categorical_crossentropy(y_true=y, y_pred=y_pred)
- loss = tf.reduce_mean(loss)
- print("batch %d: loss %f" % (batch_index, loss.numpy()))
- grads = tape.gradient(loss, model.variables)
- optimizer.apply_gradients(grads_and_vars=zip(grads, model.variables))
关于文本生成的过程有一点需要特别注意。之前,我们一直使用 tf.argmax() 函数,将对应概率最大的值作为预测值。然而对于文本生成而言,这样的预测方式过于绝对,会使得生成的文本失去丰富性。于是,我们使用 np.random.choice() 函数按照生成的概率分布取样。这样,即使是对应概率较小的字符,也有机会被取样到。同时,我们加入一个 temperature 参数控制分布的形状,参数值越大则分布越平缓(最大值和最小值的差值越小),生成文本的丰富度越高;参数值越小则分布越陡峭,生成文本的丰富度越低。
- def predict(self, inputs, temperature=1.):
- batch_size, _ = tf.shape(inputs)
- logits = self(inputs, from_logits=True)
- prob = tf.nn.softmax(logits / temperature).numpy()
- return np.array([np.random.choice(self.num_chars, p=prob[i, :])
- for i in range(batch_size.numpy())])
通过这种方式进行 “滚雪球” 式的连续预测,即可得到生成文本。
- X_, _ = data_loader.get_batch(seq_length, 1)
- for diversity in [0.2, 0.5, 1.0, 1.2]:
- X = X_
- print("diversity %f:" % diversity)
- for t in range(400):
- y_pred = model.predict(X, diversity)
- print(data_loader.indices_char[y_pred[0]], end='', flush=True)
- X = np.concatenate([X[:, 1:], np.expand_dims(y_pred, axis=1)], axis=-1)
- print("\n")
生成的文本如下:
- diversity 0.200000:
- conserted and conseive to the conterned to it is a self--and seast and the selfes as a seast the expecience and and and the self--and the sered is a the enderself and the sersed and as a the concertion of the series of the self in the self--and the serse and and the seried enes and seast and the sense and the eadure to the self and the present and as a to the self--and the seligious and the enders
- diversity 0.500000:
- can is reast to as a seligut and the complesed
- has fool which the self as it is a the beasing and us immery and seese for entoured underself of the seless and the sired a mears and everyther to out every sone thes and reapres and seralise as a streed liees of the serse to pease the cersess of the selung the elie one of the were as we and man one were perser has persines and conceity of all self-el
- diversity 1.000000:
- entoles by
- their lisevers de weltaale, arh pesylmered, and so jejurted count have foursies as is
- descinty iamo; to semplization refold, we dancey or theicks-welf--atolitious on his
- such which
- here
- oth idey of pire master, ie gerw their endwit in ids, is an trees constenved mase commars is leed mad decemshime to the mor the elige. the fedies (byun their ope wopperfitious--antile and the it as the f
- diversity 1.200000:
- cain, elvotidue, madehoublesily
- inselfy!--ie the rads incults of to prusely le]enfes patuateded:.--a coud--theiritibaior "nrallysengleswout peessparify oonsgoscess teemind thenry ansken suprerial mus, cigitioum: 4reas. whouph: who
- eved
- arn inneves to sya" natorne. hag open reals whicame oderedte,[fingo is
- zisternethta simalfule dereeg hesls lang-lyes thas quiin turjentimy; periaspedey tomm--whach
- 5
- 此处的任务及实现参考了 https://github.com/keras-team/keras/blob/master/examples/lstm_text_generation.py
循环神经网络的工作过程
循环神经网络是一个处理时间序列数据的神经网络结构,也就是说,我们需要在脑海里有一根时间轴,循环神经网络具有初始状态 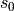 ,在每个时间点
,在每个时间点 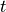 迭代对当前时间的输入
迭代对当前时间的输入 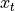 进行处理,修改自身的状态
进行处理,修改自身的状态 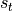 ,并进行输出
,并进行输出 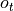 。
。
循环神经网络的核心是状态  ,是一个特定维数的向量,类似于神经网络的 “记忆”。在
,是一个特定维数的向量,类似于神经网络的 “记忆”。在 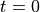 的初始时刻,
的初始时刻,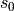 被赋予一个初始值(常用的为全 0 向量)。然后,我们用类似于递归的方法来描述循环神经网络的工作过程。即在
被赋予一个初始值(常用的为全 0 向量)。然后,我们用类似于递归的方法来描述循环神经网络的工作过程。即在 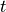 时刻,我们假设
时刻,我们假设 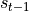 已经求出,关注如何在此基础上求出
已经求出,关注如何在此基础上求出 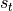 :
:
对输入向量
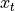 通过矩阵
通过矩阵 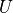 进行线性变换,
进行线性变换,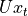 与状态 s 具有相同的维度;
与状态 s 具有相同的维度;对
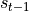 通过矩阵
通过矩阵 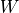 进行线性变换,
进行线性变换,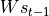 与状态 s 具有相同的维度;
与状态 s 具有相同的维度;将上述得到的两个向量相加并通过激活函数,作为当前状态
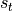 的值,即
的值,即 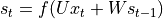 。也就是说,当前状态的值是上一个状态的值和当前输入进行某种信息整合而产生的;
。也就是说,当前状态的值是上一个状态的值和当前输入进行某种信息整合而产生的;对当前状态
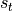 通过矩阵
通过矩阵 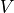 进行线性变换,得到当前时刻的输出
进行线性变换,得到当前时刻的输出 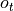 。
。
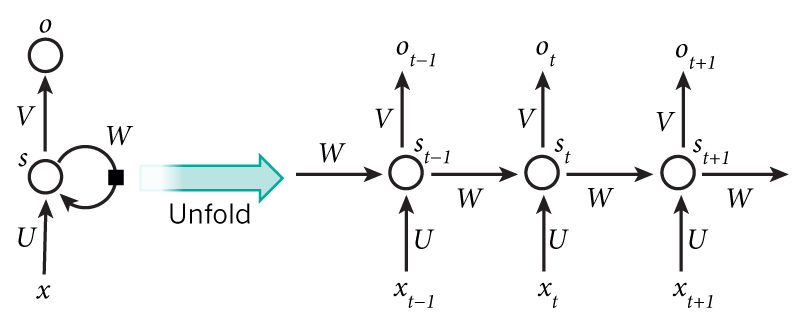 RNN 工作过程图示(来自 http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/)
RNN 工作过程图示(来自 http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/)
我们假设输入向量 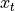 、状态
、状态  和输出向量
和输出向量 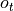 的维度分别为
的维度分别为 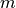 、
、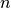 、
、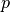 ,则
,则 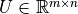 、
、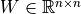 、
、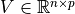 。
。
上述为最基础的 RNN 原理介绍。在实际使用时往往使用一些常见的改进型,如LSTM(长短期记忆神经网络,解决了长序列的梯度消失问题,适用于较长的序列)、GRU等。
