卷积神经网络（CNN）

卷积神经网络（CNN）
- 使用Keras实现卷积神经网络
- 使用Keras中预定义的经典卷积神经网络结构

卷积神经网络（Convolutional Neural Network, CNN）是一种结构类似于人类或动物的视觉系统的人工神经网络，包含一个或多个卷积层（Convolutional Layer）、池化层（Pooling Layer）和全连接层（Fully-connected Layer）。

基础知识和原理

台湾大学李宏毅教授的《机器学习》课程的 Convolutional Neural Network 一章；
UFLDL 教程 Convolutional Neural Network 一节；
斯坦福课程 CS231n: Convolutional Neural Networks for Visual Recognition 中的 “Module 2: Convolutional Neural Networks” 部分。

使用Keras实现卷积神经网络

卷积神经网络的一个示例实现如下所示，和上节中的多层感知机在代码结构上很类似，只是新加入了一些卷积层和池化层。这里的网络结构并不是唯一的，可以增加、删除或调整 CNN 的网络结构和参数，以达到更好的性能。

class CNN(tf.keras.Model):
    def __init__(self):
        super().__init__()
        self.conv1 = tf.keras.layers.Conv2D(
            filters=32,             # 卷积层神经元（卷积核）数目
            kernel_size=[5, 5],     # 感受野大小
            padding='same',         # padding策略（vaild 或 same）
            activation=tf.nn.relu   # 激活函数
        )
        self.pool1 = tf.keras.layers.MaxPool2D(pool_size=[2, 2], strides=2)
        self.conv2 = tf.keras.layers.Conv2D(
            filters=64,
            kernel_size=[5, 5],
            padding='same',
            activation=tf.nn.relu
        )
        self.pool2 = tf.keras.layers.MaxPool2D(pool_size=[2, 2], strides=2)
        self.flatten = tf.keras.layers.Reshape(target_shape=(7 * 7 * 64,))
        self.dense1 = tf.keras.layers.Dense(units=1024, activation=tf.nn.relu)
        self.dense2 = tf.keras.layers.Dense(units=10)
 
    def call(self, inputs):
        x = self.conv1(inputs)                  # [batch_size, 28, 28, 32]
        x = self.pool1(x)                       # [batch_size, 14, 14, 32]
        x = self.conv2(x)                       # [batch_size, 14, 14, 64]
        x = self.pool2(x)                       # [batch_size, 7, 7, 64]
        x = self.flatten(x)                     # [batch_size, 7 * 7 * 64]
        x = self.dense1(x)                      # [batch_size, 1024]
        x = self.dense2(x)                      # [batch_size, 10]
        output = tf.nn.softmax(x)
        return output

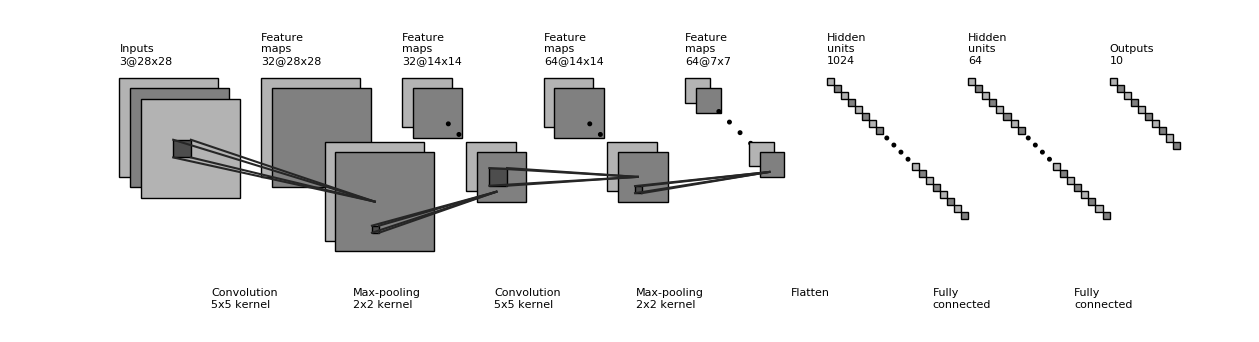../../_images/cnn.png 示例代码中的 CNN 结构图示

将前节的 model = MLP() 更换成 model = CNN() ，输出如下:

test accuracy: 0.988100

可以发现准确率相较于前节的多层感知机有非常显著的提高。事实上，通过改变模型的网络结构（比如加入 Dropout 层防止过拟合），准确率还有进一步提升的空间。

使用Keras中预定义的经典卷积神经网络结构

tf.keras.applications 中有一些预定义好的经典卷积神经网络结构，如 VGG16 、 VGG19 、 ResNet 、 MobileNet 等。我们可以直接调用这些经典的卷积神经网络结构（甚至载入预训练的参数），而无需手动定义网络结构。

例如，我们可以使用以下代码来实例化一个 MobileNetV2 网络结构：

model = tf.keras.applications.MobileNetV2()

当执行以上代码时，TensorFlow会自动从网络上下载 MobileNetV2 网络结构，因此在第一次执行代码时需要具备网络连接。每个网络结构具有自己特定的详细参数设置，一些共通的常用参数如下：

input_shape ：输入张量的形状（不含第一维的Batch），大多默认为 224 × 224 × 3 。一般而言，模型对输入张量的大小有下限，长和宽至少为 32 × 32 或 75 × 75 ；
include_top ：在网络的最后是否包含全连接层，默认为 True ；
weights ：预训练权值，默认为 'imagenet' ，即为当前模型载入在ImageNet数据集上预训练的权值。如需随机初始化变量可设为 None ；
classes ：分类数，默认为1000。修改该参数需要 include_top 参数为 True 且 weights 参数为 None 。

各网络模型参数的详细介绍可参考 Keras文档。

以下展示一个例子，使用 MobileNetV2 网络在 tf_flowers 五分类数据集上进行训练（为了代码的简短高效，在该示例中我们使用了 TensorFlow Datasets 和 tf.data 载入和预处理数据）。通过将 weights 设置为 None ，我们随机初始化变量而不使用预训练权值。同时将 classes 设置为5，对应于5分类的数据集。

import tensorflow as tf
import tensorflow_datasets as tfds
 
num_batches = 1000
batch_size = 50
learning_rate = 0.001
 
dataset = tfds.load("tf_flowers", split=tfds.Split.TRAIN, as_supervised=True)
dataset = dataset.map(lambda img, label: (tf.image.resize(img, [224, 224]) / 255.0, label)).shuffle(1024).batch(32)
model = tf.keras.applications.MobileNetV2(weights=None, classes=5)
optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate)
for images, labels in dataset:
    with tf.GradientTape() as tape:
        labels_pred = model(images)
        loss = tf.keras.losses.sparse_categorical_crossentropy(y_true=labels, y_pred=labels_pred)
        loss = tf.reduce_mean(loss)
        print("loss %f" % loss.numpy())
    grads = tape.gradient(loss, model.trainable_variables)
    optimizer.apply_gradients(grads_and_vars=zip(grads, model.trainable_variables))

后文的部分章节（如分布式训练）中，我们也会直接调用这些经典的网络结构来进行训练。

卷积层和池化层的工作原理

卷积层（Convolutional Layer，以 tf.keras.layers.Conv2D 为代表）是 CNN 的核心组件，其结构与大脑的视觉皮层有类似之处。

回忆我们之前建立的神经细胞的计算模型以及全连接层，我们默认每个神经元与上一层的所有神经元相连。不过，在视觉皮层的神经元中，情况并不是这样。你或许在生物课上学习过 感受野 （Receptive Field）这一概念，即视觉皮层中的神经元并非与前一层的所有神经元相连，而只是感受一片区域内的视觉信号，并只对局部区域的视觉刺激进行反应。CNN 中的卷积层正体现了这一特性。

例如，下图是一个 7×7 的单通道图片信号输入：

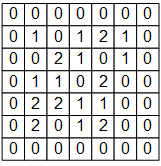
../../_images/conv_image.png

如果使用之前基于全连接层的模型，我们需要让每个输入信号对应一个权值，即建模一个神经元需要 7×7=49 个权值（加上偏置项是50个），并得到一个输出信号。如果一层有 N 个神经元，我们就需要 49N 个权值，并得到 N 个输出信号。

而在 CNN 的卷积层中，我们这样建模一个卷积层的神经元：

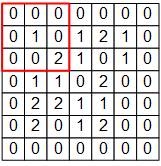
../../_images/conv_field.png

图中 3×3 的红框代表该神经元的感受野。由此，我们只需 3×3=9 个权值 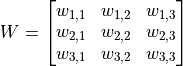$W = \begin{bmatrix}w_{1, 1} & w_{1, 2} & w_{1, 3} \\w_{2, 1} & w_{2, 2} & w_{2, 3} \\w_{3, 1} & w_{3, 2} & w_{3, 3}\end{bmatrix}$ ，外加1个偏置项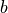，即可得到一个输出信号。例如，对于红框所示的位置，输出信号即为对矩阵 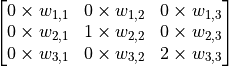$\begin{bmatrix}0 \times w_{1, 1} & 0 \times w_{1, 2} & 0 \times w_{1, 3} \\0 \times w_{2, 1} & 1 \times w_{2, 2} & 0 \times w_{2, 3} \\0 \times w_{3, 1} & 0 \times w_{3, 2} & 2 \times w_{3, 3}\end{bmatrix}$ 的所有元素求和并加上偏置项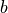，记作 $a_{1, 1}$ 。

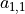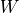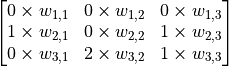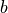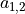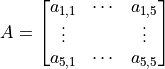不过，3×3 的范围显然不足以处理整个图像，因此我们使用滑动窗口的方法。使用相同的参数，但将红框在图像中从左到右滑动，进行逐行扫描，每滑动到一个位置就计算一个值。例如，当红框向右移动一个单位时，我们计算矩阵 $\begin{bmatrix}0 \times w_{1, 1} & 0 \times w_{1, 2} & 0 \times w_{1, 3} \\1 \times w_{2, 1} & 0 \times w_{2, 2} & 1 \times w_{2, 3} \\0 \times w_{3, 1} & 2 \times w_{3, 2} & 1 \times w_{3, 3}\end{bmatrix}$ 的所有元素的和加上偏置项，记作 $a_{1, 2}$ 。由此，和一般的神经元只能输出 1 个值不同，这里的卷积层神经元可以输出一个 5×5 的矩阵 $A = \begin{bmatrix}a_{1, 1} & \cdots & a_{1, 5} \\ \vdots & & \vdots \\ a_{5, 1} & \cdots & a_{5, 5}\end{bmatrix}$ 。

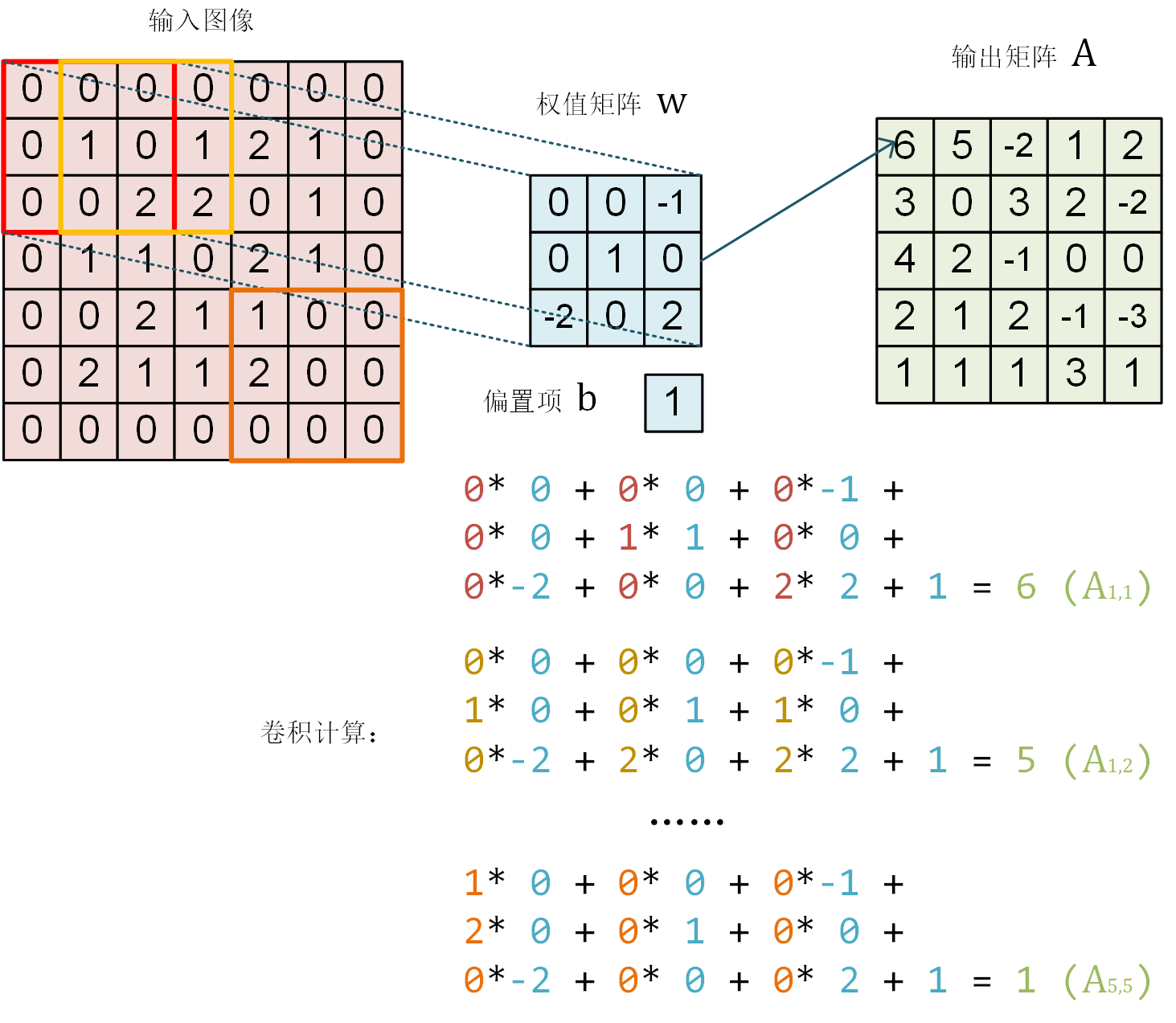../../_images/conv_procedure.png 卷积示意图。一个单通道的 7×7 图像在通过一个感受野为 3×3 ，参数为10个的卷积层神经元后，得到 5×5 的矩阵作为卷积结果。

下面，我们使用TensorFlow来验证一下上图的计算结果。

将上图中的输入图像、权值矩阵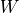和偏置项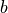表示为NumPy数组 image , W , b 如下：

# TensorFlow 的图像表示为 [图像数目，长，宽，色彩通道数] 的四维张量
# 这里我们的输入图像 image 的张量形状为 [1, 7, 7, 1]
image = np.array([[
    [0, 0, 0, 0, 0, 0, 0],
    [0, 1, 0, 1, 2, 1, 0],
    [0, 0, 2, 2, 0, 1, 0],
    [0, 1, 1, 0, 2, 1, 0],
    [0, 0, 2, 1, 1, 0, 0],
    [0, 2, 1, 1, 2, 0, 0],
    [0, 0, 0, 0, 0, 0, 0]
]], dtype=np.float32)
image = np.expand_dims(image, axis=-1)  
W = np.array([[
    [ 0, 0, -1], 
    [ 0, 1, 0 ], 
    [-2, 0, 2 ]
]], dtype=np.float32)
b = np.array([1], dtype=np.float32)

然后建立一个仅有一个卷积层的模型，用 W 和 b 初始化 4 ：

model = tf.keras.models.Sequential([
    tf.keras.layers.Conv2D(
        filters=1,              # 卷积层神经元（卷积核）数目
        kernel_size=[3, 3],     # 感受野大小
        kernel_initializer=tf.constant_initializer(W),
        bias_initializer=tf.constant_initializer(b)
    )]
)

最后将图像数据 image 输入模型，打印输出：

output = model(image)
print(tf.squeeze(output))

程序运行结果为：

tf.Tensor(
[[ 6.  5. -2.  1.  2.]
 [ 3.  0.  3.  2. -2.]
 [ 4.  2. -1.  0.  0.]
 [ 2.  1.  2. -1. -3.]
 [ 1.  1.  1.  3.  1.]], shape=(5, 5), dtype=float32)

可见与上图中矩阵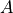的值一致。

还有一个问题，以上假设图片都只有一个通道（例如灰度图片），但如果图像是彩色的（例如有 RGB 三个通道）该怎么办呢？此时，我们可以为每个通道准备一个 3×3 的权值矩阵，即一共有 3×3×3=27 个权值。对于每个通道，均使用自己的权值矩阵进行处理，输出时将多个通道所输出的值进行加和即可。

可能有读者会注意到，按照上述介绍的方法，每次卷积后的结果相比于原始图像而言，四周都会“少一圈”。比如上面 7×7 的图像，卷积后变成了 5×5 ，这有时会为后面的工作带来麻烦。因此，我们可以设定padding策略。在 tf.keras.layers.Conv2D 中，当我们将 padding 参数设为 same 时，会将周围缺少的部分使用0补齐，使得输出的矩阵大小和输入一致。

最后，既然我们可以使用滑动窗口的方法进行卷积，那么每次滑动的步长是不是可以设置呢？答案是肯定的。通过 tf.keras.layers.Conv2D 的 strides 参数即可设置步长（默认为1）。比如，在上面的例子中，如果我们将步长设定为2，输出的卷积结果即会是一个3×3的矩阵。

事实上，卷积的形式多种多样，以上的介绍只是其中最简单和基础的一种。更多卷积方式的示例可见 Convolution arithmetic 。

池化层（Pooling Layer）的理解则简单得多，其可以理解为对图像进行降采样的过程，对于每一次滑动窗口中的所有值，输出其中的最大值（MaxPooling）、均值或其他方法产生的值。例如，对于一个三通道的 16×16 图像（即一个 16163 的张量），经过感受野为 2×2，滑动步长为 2 的池化层，则得到一个 883 的张量。

4
这里使用了较为简易的Sequential模式建立模型，具体介绍见后文。