- 7.17.拓扑排序
7.17.拓扑排序
为了表明计算机科学家可以把任何东西变成一个图问题,让我们考虑做一批煎饼的问题。 菜谱真的很简单:1个鸡蛋,1杯煎饼粉,1汤匙油 和 3/4 杯牛奶。 要制作煎饼,你必须加热炉子,将所有的成分混合在一起,勺子搅拌。 当开始冒泡,你把它们翻过来,直到他们底部变金黄色。 在你吃煎饼之前,你会想要加热一些糖浆。 Figure 27将该过程示为图。
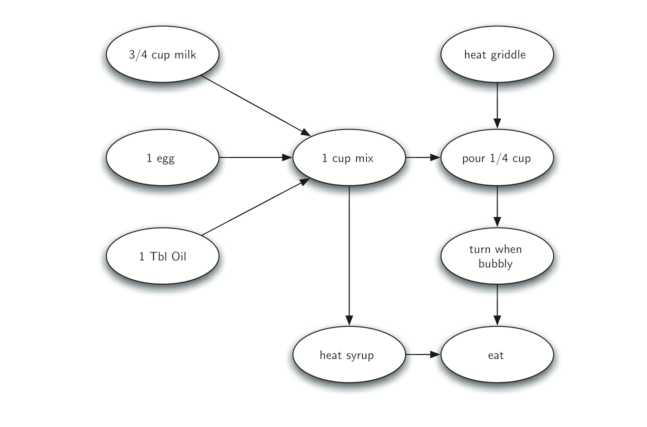
Figure 27
制作煎饼的困难是知道先做什么。从 Figure 27 可以看出,你可以从加热煎饼开始,或通过添加任何成分到煎饼。为了帮助我们决定应该做的每一个步骤的精确顺序,我们转向一个图算法称为 拓扑排序。
拓扑排序采用有向无环图,并且产生所有其顶点的线性排序,使得如果图 G 包含边
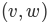 ,则顶点 v 在排序中位于顶点 w 之前。定向非循环图在许多应用中使用以指示事件的优先级。制作煎饼只是一个例子;其他示例包括软件项目计划,用于数据库查询的优先图以及乘法矩阵。
,则顶点 v 在排序中位于顶点 w 之前。定向非循环图在许多应用中使用以指示事件的优先级。制作煎饼只是一个例子;其他示例包括软件项目计划,用于数据库查询的优先图以及乘法矩阵。
拓扑排序是深度优先搜索的简单但有用的改造。拓扑排序的算法如下:
- 对于某些图
g调用dfs(g)。我们想要调用深度优先搜索的主要原因是计算每个顶点的完成时间。 - 以完成时间的递减顺序将顶点存储在列表中。
- 返回有序列表作为拓扑排序的结果。Figure 28 展示了在 Figure 26 所示的薄煎饼制作图上由
dfs构建的深度优先森林。
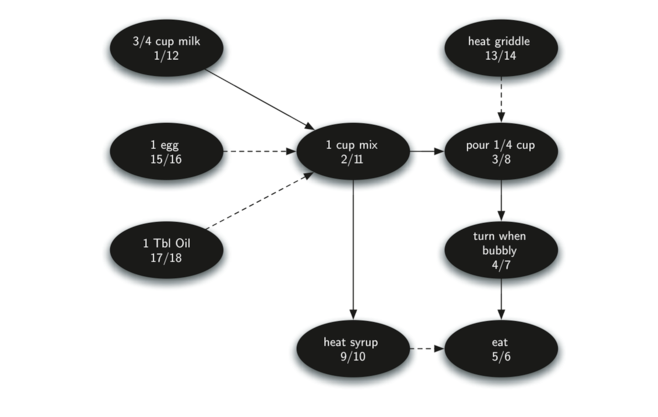
Figure 28
最后,Figure 29 展示了将拓扑排序算法应用于我们的图形的结果。 现在所有的分支已被删除,我们知道确切的做煎饼的步骤顺序。

Figure 29
