• 3.14.模拟：打印机
    • 3.14.1.主要模拟步骤
    • 3.14.2 Python 实现
    • 3.14.3.讨论

    3.14.模拟：打印机

    一个更有趣的模拟是允许我们研究本节前面描述的打印机的行为，回想一下，当学生向共享打印机发送打印任务时，任务被放置在队列中以便以先来先服务的方式被处理。此配置会出现许多问题。其中最重要的点可能是打印机是否能够处理一定量的工作。如果它不能，学生将等待太长时间打印，可能会错过他们的下一节课。

    在计算机科学实验室里考虑下面的情况。平均每天大约10名学生在任何给定时间在实验室工作。这些学生通常在此期间打印两次，这些任务的长度范围从1到20页。实验室中的打印机较旧，每分钟以草稿质量可以处理10页。打印机可以切换以提供更好的质量，但是它将每分钟只能处理五页。较慢的打印速度可能会使学生等待太久。应使用什么页面速率？

    我们可以通过建立一个模拟实验来决定。我们将需要为学生，打印任务和打印机构建表现表示（Figure 4）。当学生提交打印任务时，我们将把他们添加到等待列表中，一个打印任务的队列。 当打印机完成任务时，它将检查队列，以检查是否有剩余的任务要处理。我们感兴趣的是学生等待他们的论文打印的平均时间。这等于任务在队列中等待的平均时间量。

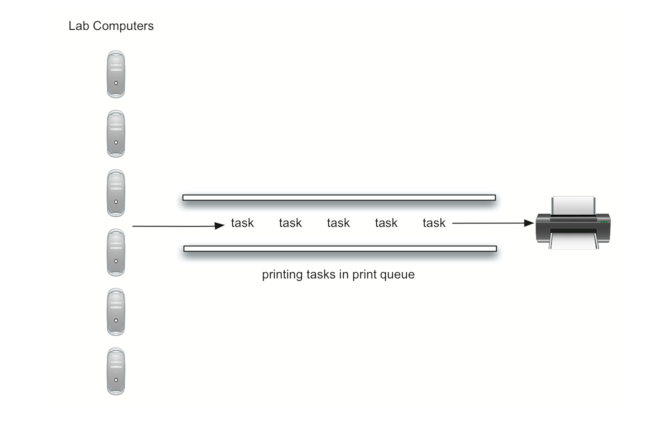
    3.14.模拟：打印机.figure4

    Figure 4

    为了为这种情况建模，我们需要使用一些概率。例如，学生可以打印长度从 1 到 20 页的纸张。如果从 1 到 20 的每个长度有同样的可能性，则可以通过使用 1 和 20 之间的随机数来模拟打印任务的实际长度。这意味着出现从 1 到 20 的任何长度的机会是平等的。

    如果实验室中有 10 个学生，每人打印两次，则平均每小时有 20 个打印任务。 在任何给定的秒，打印任务将被创建的机会是什么？ 回答这个问题的方法是考虑任务与时间的比率。每小时 20 个任务意味着平均每 180 秒将有一个任务：

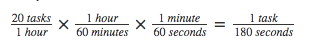
    3.14.模拟：打印机.figure1

    对于每一秒，我们可以通过生成 1 到 180 之间的随机数来模拟打印任务发生的机会。如果数字是 180，我们说一个任务已经创建。请注意，可能会在一下子创建许多任务，或者需要等待一段时间才有任务。这就是模拟的本质。你想模拟真实的情况就需要尽可能接近一般参数。

    3.14.1.主要模拟步骤

    • 创建打印任务的队列，每个任务都有个时间戳。队列启动的时候为空。
    • 每秒（currentSecond）：
    • 是否创建新的打印任务？如果是，将 currentSecond 作为时间戳添加到队列。
    • 如果打印机不忙并且有任务在等待
      • 从打印机队列中删除一个任务并将其分配给打印机
      • 从 currentSecond 中减去时间戳，以计算该任务的等待时间。
      • 将该任务的等待时间附件到列表中稍后处理。
      • 根据打印任务的页数，确定需要多少时间。
    • 打印机需要一秒打印，所以得从该任务的所需的等待时间减去一秒。
    • 如果任务已经完成，换句话说，所需的时间已经达到零，打印机空闲。
      • 模拟完成后，从生成的等待时间列表中计算平均等待时间。

    3.14.2 Python 实现

    为了设计此模拟，我们将为上述三个真实世界对象创建类：Printer, Task, PrintQueue

    Printer 类（Listing 2）需要跟踪它当前是否有任务。如果有，则它处于忙碌状态（13-17 行），并且可以从任务的页数计算所需的时间。构造函数允许初始化每分钟页面的配置，tick 方法将内部定时器递减直到打印机设置为空闲(11 行)

    1. class Printer:
    2.     def __init__(self, ppm):
    3.         self.pagerate = ppm
    4.         self.currentTask = None
    5.         self.timeRemaining = 0
    7.     def tick(self):
    8.         if self.currentTask != None:
    9.             self.timeRemaining = self.timeRemaining - 1
    10.             if self.timeRemaining <= 0:
    11.                 self.currentTask = None
    13.     def busy(self):
    14.         if self.currentTask != None:
    15.             return True
    16.         else:
    17.             return False
    19.     def startNext(self,newtask):
    20.         self.currentTask = newtask
    21.         self.timeRemaining = newtask.getPages() * 60/self.pagerate

    Listing 2

    Task 类（Listing 3）表示单个打印任务。创建任务时，随机数生成器将提供 1 到 20 页的长度。我们选择使用随机模块中的 randrange 函数。

    1. >>> import random
    2. >>> random.randrange(1,21)
    3. 18
    4. >>> random.randrange(1,21)
    5. 8
    6. >>>

    每个任务还需要保存一个时间戳用于计算等待时间。此时间戳将表示任务被创建并放置到打印机队列中的时间。可以使用 waitTime 方法来检索在打印开始之前队列中花费的时间。

    1. import random
    3. class Task:
    4.     def __init__(self,time):
    5.         self.timestamp = time
    6.         self.pages = random.randrange(1,21)
    8.     def getStamp(self):
    9.         return self.timestamp
    11.     def getPages(self):
    12.         return self.pages
    14.     def waitTime(self, currenttime):
    15.         return currenttime - self.timestamp

    Listing 3

    Listing 4 实现了上述算法。PrintQueue 对象是我们现有队列 ADT 的一个实例。newPrintTask 决定是否创建一个新的打印任务。我们再次选择使用随机模块的 randrange 函数返回 1 到 180 之间的随机整数。打印任务每 180 秒到达一次。通过从随机整数（32 行）的范围中任意选择，我们可以模拟这个随机事件。模拟功能允许我们设置打印机的总时间和每分钟的页数。

    1. from pythonds.basic.queue import Queue
    3. import random
    5. def simulation(numSeconds, pagesPerMinute):
    7.     labprinter = Printer(pagesPerMinute)
    8.     printQueue = Queue()
    9.     waitingtimes = []
    11.     for currentSecond in range(numSeconds):
    13.       if newPrintTask():
    14.          task = Task(currentSecond)
    15.          printQueue.enqueue(task)
    17.       if (not labprinter.busy()) and (not printQueue.isEmpty()):
    18.         nexttask = printQueue.dequeue()
    19.         waitingtimes.append(nexttask.waitTime(currentSecond))
    20.         labprinter.startNext(nexttask)
    22.       labprinter.tick()
    24.     averageWait=sum(waitingtimes)/len(waitingtimes)
    25.     print("Average Wait %6.2f secs %3d tasks remaining."%(averageWait,printQueue.size()))
    27. def newPrintTask():
    28.     num = random.randrange(1,181)
    29.     if num == 180:
    30.         return True
    31.     else:
    32.         return False
    34. for i in range(10):
    35.     simulation(3600,5)

    Listing 4

    当我们运行模拟时，我们不应该担心每次的结果不同。这是由于随机数的概率性质决定的。 因为模拟的参数可以被调整，我们对调整后可能发生的趋势感兴趣。 这里有一些结果。

    首先，我们将使用每分钟五页的页面速率运行模拟 60 分钟（3,600秒）。 此外，我们将进行 10 次独立试验。记住，因为模拟使用随机数，每次运行将返回不同的结果。

    1. >>>for i in range(10):
    2.       simulation(3600,5)
    4. Average Wait 165.38 secs 2 tasks remaining.
    5. Average Wait  95.07 secs 1 tasks remaining.
    6. Average Wait  65.05 secs 2 tasks remaining.
    7. Average Wait  99.74 secs 1 tasks remaining.
    8. Average Wait  17.27 secs 0 tasks remaining.
    9. Average Wait 239.61 secs 5 tasks remaining.
    10. Average Wait  75.11 secs 1 tasks remaining.
    11. Average Wait  48.33 secs 0 tasks remaining.
    12. Average Wait  39.31 secs 3 tasks remaining.
    13. Average Wait 376.05 secs 1 tasks remaining.

    在运行 10 次实验后，我们可以看到，平均等待时间为 122.09 秒。 还可以看到平均等待时间有很大的变化，最小值为 17.27 秒，最大值为 376.05 秒。 你也可能注意到，只有两种情况所有任务都完成。

    现在，我们将页面速率调整为每分钟 10 页，再次运行 10 次测试，页面速度更快，我们希望在一小时内完成更多的任务。

    1. >>>for i in range(10):
    2.       simulation(3600,10)
    4. Average Wait   1.29 secs 0 tasks remaining.
    5. Average Wait   7.00 secs 0 tasks remaining.
    6. Average Wait  28.96 secs 1 tasks remaining.
    7. Average Wait  13.55 secs 0 tasks remaining.
    8. Average Wait  12.67 secs 0 tasks remaining.
    9. Average Wait   6.46 secs 0 tasks remaining.
    10. Average Wait  22.33 secs 0 tasks remaining.
    11. Average Wait  12.39 secs 0 tasks remaining.
    12. Average Wait   7.27 secs 0 tasks remaining.
    13. Average Wait  18.17 secs 0 tasks remaining.

    3.14.3.讨论

    我们试图回答一个问题，即当前打印机是否可以处理任务负载，如果它设置为打印更好的质量，较慢的页面速率。我们采用的方法是编写一个模拟打印任务作为各种页数和到达时间的随机事件的模拟。

    上面的输出显示，每分钟打印 5 页，平均等待时间从低的 17 秒到高的 376 秒（约 6 分钟）。使用更快的打印速率，低值为 1 秒，高值仅为 28。此外，在 10 次运行中的 8 次，每分钟 5 页，打印任务在结束时仍在队列中等待。

    因此，我们说减慢打印机的速度以获得更好的质量可能不是一个好主意。学生们不能等待他们的论文打印完，特别是当他们需要到下一个班级。六分钟的等待时间太长了。

    这种类型的模拟分析允许我们回答许多问题，通常被称为“如果”的问题。我们需要做的是改变模拟使用的参数，我们可以模拟任何数量。例如

    • 如果入学人数增加，平均学生人数增加 20 人 该怎么办？
    • 如果是星期六，学生不需要上课怎么办？他们能负担得了吗？
    • 如果平均打印任务的大小减少了，由于 Python 是一个强大的语言，程序往往要短得多？ 这些问题都可以通过修改上述模拟来回答。然而，重要的是要记住，模拟有效取决于构建它的假设是没问题的。关于每小时打印任务的数量和每小时的学生数量的真实数据对于构建鲁棒性的模拟是必要的。