- 1.13.Python中面向对象编程:定义类
- 1.13.1.一个分数类
- 1.13.2.继承:逻辑门和电路
1.13.Python中面向对象编程:定义类
我们之前说过,Python是一种面向对象的编程语言。到目前为止,我们已经使用了许多内置类来显示示例数据和控制结构。 面向对象编程语言中最强大的功能之一是允许程序员(问题解决者)创建新类,以模拟解决问题所需的数据。
请记住,我们使用抽象数据类型来提供数据对象的外观(其状态)及其可以执行的操作(其方法)的逻辑描述。 通过构建实现抽象数据类型的类,程序员可以利用抽象过程,同时提供在程序中实际使用抽象所需的详细信息。 每当我们想要实现抽象数据类型时,我们都会使用新类。
1.13.1.一个分数类
一个非常常见的例子,展示实现用户定义的类的细节,就是构造一个类来实现抽象的分数数据类型。我们已经看到Python提供了许多供我们使用的数字类。然而,有时候,能够创建“看起来像”分数的数据对象是最合适的。
像3/5这样的分数由两部分组成。最上面的值,也就是分子,可以是任意整数。底部的值,叫做分母,可以是大于0的整数(负分数有负的分子)。尽管可以为任何分数创建浮点近似,在这种情况下,我们想把分数表示成一个精确的值。
Fraction类型的操作将允许Fraction数据对象的行为与任何其他数值一样。 我们需要能够对分数进行加,减,乘和除。 我们还希望能够使用标准的“斜杠”形式显示分数,例如3/5。 此外,所有分数方法都应以最低项返回结果,这样无论执行何种计算,我们总是以最常见的形式结束。
在Python中,我们通过提供一个名称和一组在语法上类似于函数定义的方法定义来定义一个新类。 对于这个例子,
class Fraction:#the methods go here
为我们提供了定义方法的框架。 所有类应提供的第一个方法是构造函数。 构造函数定义了数据对象的创建方式。 要创建Fraction对象,我们需要提供两个数据,分子和分母。 在Python中,构造函数方法始终称为init (init之前和之后的两个下划线),如Listing 2所示。
Listing 1
class Fraction:def __init__(self,top,bottom):self.num = topself.den = bottom
请注意,形式参数列表包含三个项目(self,top,bottom)。 self是一个特殊参数,将始终用作返回对象本身的引用。 它必须始终是第一个形式参数; 但是,在调用时永远不会给出实际的参数值。 如前所述,分数需要两个状态数据,即分子和分母。构造函数中的符号self.num定义了Fraction对象,使其具有名为num的内部数据对象作为其状态的一部分。同样,self.den创建了分母。两个正式参数做初始化赋值,允许新的分数对象知道它的起始值。
要创建分数类的实例,我们必须调用构造函数。这发生在使用类名并传递必要状态的实际值(请注意,我们从不直接调用init)。 例如,
myfraction = Fraction(3,5)
创建一个名为myfraction的对象,表示分数3/5(五分之三)。 Figure 5显示了此对象,因为它当前已实现。
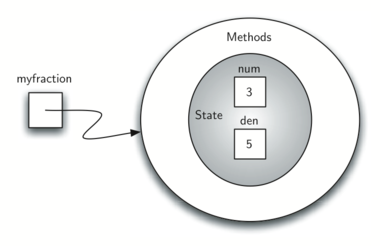
Figure 5
我们需要做的下一件事是实现抽象数据类型所需的行为。 首先,考虑一下当我们尝试打印Fraction对象时会发生什么。
>>> myf = Fraction(3,5)>>> print(myf)<__main__.Fraction instance at 0x409b1acc>
fraction对象myf不知道如何响应此打印请求。 print函数要求对象将自身转换为字符串,以便可以将字符串写入输出。 myf唯一的选择是显示存储在变量中的实际引用(地址本身)。 这不是我们想要的。
我们有两种方法可以解决这个问题。 一种是定义一个名为show的方法,它允许Fraction对象将自己打印为字符串。 我们可以实现此方法,如Listing 3所示。如果我们像以前一样创建Fraction对象,我们可以要求它显示自己,换句话说,以适当的格式打印自己。 不幸的是,这一般不起作用。 为了使打印正常工作,我们需要告诉Fraction类如何将自身转换为字符串。 这是打印功能为了完成其工作所需要的。
Listing 3
def show(self):print(self.num,"/",self.den)
>>> myf = Fraction(3,5)>>> myf.show()3 / 5>>> print(myf)<__main__.Fraction instance at 0x40bce9ac>>>>
在Python中,所有类都提供了一组标准方法,但可能无法正常工作。 其中之一str是一种将对象转换为字符串的方法。 正如我们已经看到的,此方法的默认实现是返回实例地址字符串。我们需要做的是为这种方法提供“更好”的实现。我们会说这个实现将覆盖前一个或重新定义方法的行为。
为此,我们只需定义一个名为str的方法,并为其提供一个新的实现,如Listing 4所示。除了特殊参数self之外,该定义不需要任何其他信息。 反过来,该方法将通过让每个内部状态数据转换为字符串然后使用字符串连接在字符串之间放置/字符来构建字符串表示。 每当要求Fraction对象将其自身转换为字符串时,将返回结果字符串。 请注意使用此功能的各种方法。
Listing 4
def __str__(self):return str(self.num)+"/"+str(self.den)
>>> myf = Fraction(3,5)>>> print(myf)3/5>>> print("I ate", myf, "of the pizza")I ate 3/5 of the pizza>>> myf.__str__()'3/5'>>> str(myf)'3/5'>>>
我们可以为新的Fraction类覆盖许多其他方法。 其中一些最重要的是基本的算术运算。 我们希望能够创建两个Fraction对象,然后使用标准的“+”符号将它们添加到一起。 此时,如果我们尝试添加两个分数,我们得到以下结果:
>>> f1 = Fraction(1,4)>>> f2 = Fraction(1,2)>>> f1+f2Traceback (most recent call last):File "<pyshell#173>", line 1, in -toplevel-f1+f2TypeError: unsupported operand type(s) for +:'instance' and 'instance'>>>
如果仔细查看错误,您会发现问题是“+”运算符不理解Fraction操作数。
我们可以通过为Fraction类提供一个覆盖add方法的方法来解决这个问题。 在Python中,此方法称为add,它需要两个参数。 第一个是self,总是需要,第二个代表表达式中的另一个操作数。 例如,
f1.__add__(f2)
会要求Fraction对象f1将Fraction对象f2添加到自身。 这可以用标准符号f1 + f2编写。
两个分数必须具有相同的分母才能添加。 确保它们具有相同分母的最简单方法是简单地使用两个分母的乘积作为公分母,以便a/b + c/d = ad/bd + cb/bd = (ad + cb)/bd实现如Listing 5所示。附加函数返回一个新的Fraction对象,其总和的分子和分母。我们可以用这个方法来写一个包含分数的标准算术表达式,赋值加法的结果,然后打印我们的结果。
Listing 5
def __add__(self,otherfraction):newnum = self.num*otherfraction.den + self.den*otherfraction.numnewden = self.den * otherfraction.denreturn Fraction(newnum,newden)
>>> f1=Fraction(1,4)>>> f2=Fraction(1,2)>>> f3=f1+f2>>> print(f3)6/8>>>
添加方法可以按照我们的意愿工作,但有一点可能更好。 请注意,6/8是正确的结果(1/4 + 1/2),但它不是“最低术语”表示。 最好的代表是3/4。 为了确保我们的结果总是在最低的条件下,我们需要一个知道如何减少分数的辅助函数。 此函数需要查找最大公约数或GCD。 然后我们可以将分子和分母除以GCD,结果将减少到最低项。
用于求出最大公约数的最着名算法是欧几里德算法,将在第8章中详细讨论。欧几里德算法表明,如果n均匀地除以m,则两个整数m和n的最大公约数为n。 但是,如果n不均匀地除m,则答案是n的最大公约数,m的余数除以n。 我们将在这里简单地提供一个迭代实现(参见ActiveCode 1)。 请注意,GCD算法的此实现仅在分母为正时才有效。 这对于我们的分数类是可以接受的,因为我们已经说过负分数将由负分子表示。
ActiveCode 1
def gcd(m,n):while m%n != 0:oldm = moldn = nm = oldnn = oldm%oldnreturn nprint(gcd(20,10))
现在我们可以使用此函数来帮助减少任何分数。 为了将分数置于最低项中,我们将分子和分母除以它们的最大公约数。 因此,对于分数6/8,最大公约数为2.将顶部和底部除以2会创建一个新的分数3/4(参见Listing 6)。
Listing 6
def __add__(self,otherfraction):newnum = self.num*otherfraction.den + self.den*otherfraction.numnewden = self.den * otherfraction.dencommon = gcd(newnum,newden)return Fraction(newnum//common,newden//common)
>>> f1=Fraction(1,4)>>> f2=Fraction(1,2)>>> f3=f1+f2>>> print(f3)3/4>>>
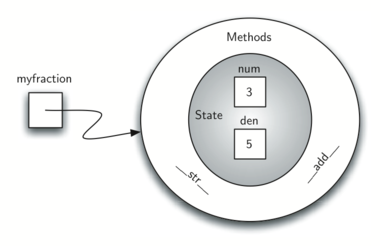
Figure 6
我们的分数对象现在有两个非常有用的方法,如Figure 6所显示。我们需要在示例Fraction类中包含的另一组方法将允许两个分数相互比较。假设我们有两个Fraction对象,f1和f2。 f1 == f2只有在引用同一个对象时才为True。具有相同分子和分母的两个不同对象在此实现下将不相等。这称为浅等式(参见Figure 7)。
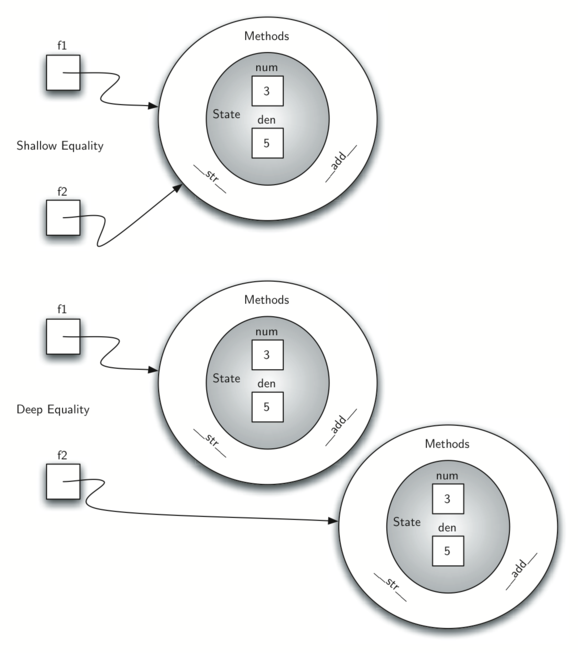
Figure 7
我们可以通过覆盖eq方法,通过相同的值创建深相等(参见Figure 7)-equality,而不是相同的引用。 eq方法是任何类中都可用的另一种标准方法。 eq方法比较两个对象,如果它们的值相同则返回True,否则返回False。
在Fraction类中,我们可以通过再次将两个分数放在通用项中然后比较分子来实现eq方法(参见Listing 7)。 值得注意的是,还有其他可以覆盖的关系运算符。 例如, le方法提供的小于或等于功能。
Listing 7
def __eq__(self, other):firstnum = self.num * other.densecondnum = other.num * self.denreturn firstnum == secondnum
到目前为止,完整的Fraction类在ActiveCode 2中显示。我们把剩下的算术和关系方法作为练习。
ActiveCode 2
def gcd(m,n):while m%n != 0:oldm = moldn = nm = oldnn = oldm%oldnreturn nclass Fraction:def __init__(self,top,bottom):self.num = topself.den = bottomdef __str__(self):return str(self.num)+"/"+str(self.den)def show(self):print(self.num,"/",self.den)def __add__(self,otherfraction):newnum = self.num*otherfraction.den + \self.den*otherfraction.numnewden = self.den * otherfraction.dencommon = gcd(newnum,newden)return Fraction(newnum//common,newden//common)def __eq__(self, other):firstnum = self.num * other.densecondnum = other.num * self.denreturn firstnum == secondnumx = Fraction(1,2)y = Fraction(2,3)print(x+y)print(x == y)
1.13.2.继承:逻辑门和电路
我们的最后一节将介绍面向对象编程的另一个重要方面。 继承是一个类与另一个类相关联的能力,与人们彼此相关的方式非常相似。 儿童继承父母的特征。 类似地,Python子类可以从父类继承特征数据和行为。 这些类通常称为子类和超类。
Figure 8显示了内置的Python集合及其相互之间的关系。 我们将这种关系结构称为继承结构。 例如,列表是有序集合的子类。 在这种情况下,我们将列表称为子级,将序列称为父级(或子类列表和超类序列)。 这通常被称为IS-A Relationship(列表IS-A游戏集合)。 这意味着列表从序列继承了重要的特征,即底层数据的排序和连接,重复和索引等操作。
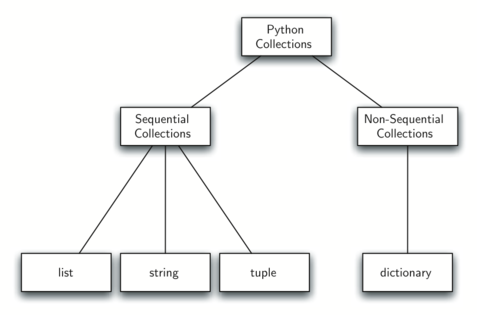
Figure 8
列表,元组和字符串都是有序集合类型。 它们都继承了常见的数据组织方式和操作。 但是,根据数据是否是同构的以及集合是否不可变,它们中的每一个都是不同的。 孩子们都从父母那里获益,并通过增加额外的特征来区分自己。
通过以这种继承方式来组织类,面向对象的编程语言允许扩展先前编写的代码以满足新情况的需要。 此外,通过以这种继承方式来组织数据,我们可以更好地理解存在的关系。 我们可以更有效地构建抽象表示。
为了进一步探索这个特性,我们将构造仿真,一个模拟数字电路的应用程序。 该模拟的基本构建块将是逻辑门。 这些电子开关代表其输入和输出之间的布尔代数关系。 通常,门具有单个输出线。 输出值取决于输入线上给出的值。
与门有两条输入线,每条输入线可以是0或1(分别代表False或True)。 如果两个输入行的值都为1,则结果输出为1.但是,如果输入行中的任何一个或两个为0,则结果为0.或者门也有两个输入行,如果一个或两个输入行都产生1 输入值的值为1.在两个输入行均为0的情况下,结果为0。
非门与其他两个门的不同之处在于它们只有一条输入线。 输出值与输入值完全相反。 如果输入上出现0,则在输出上产生1。 类似地,1产生0. Figure 9显示了这些门中的每一个通常如何表示。 每个门还有一个真值表,显示由门执行的输入到输出映射。
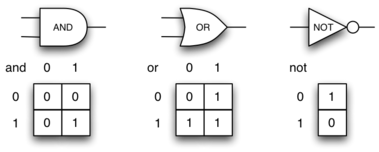
Figure 9
通过以各种模式组合这些门然后应用一组输入值,我们可以构建具有逻辑功能的电路。 Figure 10显示了一个由两个与门,一个或门和一个非门组成的电路。 来自两个与门的输出线直接馈入或门,或门产生的输出提供给非门。 如果我们将一组输入值应用于四个输入行(每个与门两个),则处理这些值并在非门的输出处显示结果。 Figure 10还显示了一个带有值的示例。
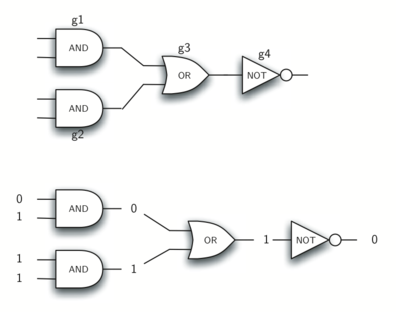
Figure 10
为了实现电路,我们将首先构建逻辑门的表示。 逻辑门很容易组织成一个类继承层次结构,如Figure 11所示。在继承结构的顶部,LogicGate类代表逻辑门的最一般特征:即门的标签和输出线。 下一级子类将逻辑门分为两个系列,即具有一个输入线的系列和具有两个输入线的系列。 在此之下,每个的特定逻辑功能出现。
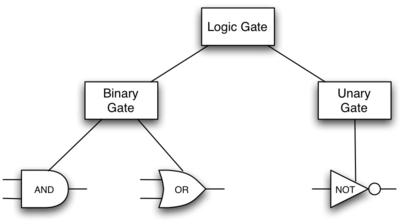
Figure 11
我们现在可以从最常见的LogicGate开始实现这些类。 如前所述,每扇门都有一个识别标签和一条输出线。 此外,我们还需要一种方法,允许门的用户从门上请求标签。。
每个逻辑门需要的另一个行为是知道其输出值的能力。 这将要求门基于当前输入执行适当的逻辑。 为了产生输出,门需要知道该逻辑具体是什么。 这意味着调用一个方法来执行逻辑计算。 完整的类如Listing 8所示。
Listing 8
class LogicGate:def __init__(self,n):self.label = nself.output = Nonedef getLabel(self):return self.labeldef getOutput(self):self.output = self.performGateLogic()return self.output
此时,我们不会实现performGateLogic函数。 原因是我们不知道每个门将如何执行自己的逻辑运算。 这些细节将包含在添加到层次结构中的每个单独的门中。 这是面向对象编程中非常强大的思想。 我们正在编写一种方法,它将使用尚不存在的代码。 参数self是对调用该方法的实际门对象的引用。 添加到层级结构中的任何新逻辑门都只需要实现performGateLogic函数,它将在适当的时候使用。 完成后,门可以提供其输出值。 这种扩展当前存在的层次结构并提供层次结构需要使用新类的特定功能的能力对于重用现有代码非常重要。
我们根据输入线的数量对逻辑门进行了分类。 与门有两条输入线。 或门也有两条输入线。 非门有一条输入线。 BinaryGate类将是LogicGate的子类,并将添加两个输入行。 UnaryGate类也将是LogicGate的子类,但只有一个输入行。 在计算机电路设计中,这些线有时被称为“引脚”,因此我们将在实现中使用该术语。
Listing 9
class BinaryGate(LogicGate):def __init__(self,n):LogicGate.__init__(self,n)self.pinA = Noneself.pinB = Nonedef getPinA(self):return int(input("Enter Pin A input for gate "+ self.getLabel()+"-->"))def getPinB(self):return int(input("Enter Pin B input for gate "+ self.getLabel()+"-->"))
Listing 10
class UnaryGate(LogicGate):def __init__(self,n):LogicGate.__init__(self,n)self.pin = Nonedef getPin(self):return int(input("Enter Pin input for gate "+ self.getLabel()+"-->"))
Listing 9和Listing 10实现了这两个类。 这两个类中的构造函数都是使用父类的init方法显式调用父类的构造函数。 在创建BinaryGate类的实例时,我们首先要初始化从LogicGate继承的任何数据项。 在这种情况下,这意味着门的标签。 然后构造函数继续添加两条输入线(pinA和pinB)。 这是构建类层次结构时应始终使用的非常常见的模式。 子类构造函数需要调用父类构造函数,然后继续使用它们自己的区分数据。
Python还有一个名为super的函数,可用于代替显式命名父类。 这是一种更通用的机制,并且被广泛使用,尤其是当一个类有多个父类时。 但是,这不是我们将在本简介中讨论的内容。 例如,在上面的示例中,LogicGate . init (self,n)可以替换为super(UnaryGate,self). init (n)。
BinaryGate类添加的唯一行为是从两个输入行获取值的能力。 由于这些值来自某些外部位置,我们只需通过输入语句询问用户即可。 除了只有一个输入行之外,UnaryGate类也会进行相同的实现。
现在我们有了一个针对门的通用类,这取决于输入行的数量,我们可以构建具有独特行为的特定门。例如,AndGate类将是BinaryGate的子类,因为与门有两条输入线。 和以前一样,构造函数的第一行调用父类构造函数(BinaryGate),后者又调用其父类构造函数(LogicGate)。 请注意,AndGate类不提供任何新数据,因为它继承了两个输入行,一个输出行和一个标签。
Listing 11
class AndGate(BinaryGate):def __init__(self,n):BinaryGate.__init__(self,n)def performGateLogic(self):a = self.getPinA()b = self.getPinB()if a==1 and b==1:return 1else:return 0
AndGate唯一需要添加的是执行前面描述的布尔操作的特定行为。 这是我们可以提供performGateLogic方法的地方。 对于AND门,此方法首先必须获取两个输入值,然后仅在两个输入值均为1时返回1.完整类如Listing 11所示。
我们可以通过创建实例并要求它计算其输出来显示AndGate类。 以下会话显示了一个AndGate对象g1,它具有内部标签“G1”。 当我们调用getOutput方法时,该对象必须首先调用其performGateLogic方法,该方法依次查询两个输入行。 提供值后,将显示正确的输出。
>>> g1 = AndGate("G1")>>> g1.getOutput()Enter Pin A input for gate G1-->1Enter Pin B input for gate G1-->00
对于或门和非门,可以进行相同的开发。 OrGate类也将是BinaryGate的子类,NotGate类将扩展UnaryGate类。 这两个类都需要提供自己的performGateLogic函数,因为这是它们的特定行为。
我们可以使用单个门,首先构造一个门类的实例,然后得到门的输出(这将反过来需要提供输入)。 例如:
>>> g2 = OrGate("G2")>>> g2.getOutput()Enter Pin A input for gate G2-->1Enter Pin B input for gate G2-->11>>> g2.getOutput()Enter Pin A input for gate G2-->0Enter Pin B input for gate G2-->00>>> g3 = NotGate("G3")>>> g3.getOutput()Enter Pin input for gate G3-->01
现在我们已经完成了基本的工作,我们可以将注意力转向构建电路。 为了创建一个电路,我们需要将门连接在一起,一个输出另一个输入。 为此,我们将实现一个名为Connector的新类。
Connector类不会驻留在门层次结构中。 然而,它将使用门层次结构,因为每个连接器将具有两个门,一个在两端(参见Figure 12)。 这种关系在面向对象编程中非常重要。 它被称为HAS-A关系。 回想一下,我们使用短语“IS-A Relationship”来表示子类与父类相关,例如UnaryGate IS-A LogicGate。
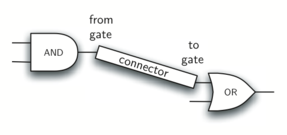
Figure 12
现在,使用Connector类,我们说连接器HAS-A LogicGate意味着连接器将包含LogicGate类的实例但不是层次结构的一部分。 在设计类时,区分具有IS-A关系(需要继承)和具有HAS-A关系(没有继承)的类非常重要。
Listing 12显示了Connector类。 每个连接器对象内的两个门实例将被称为fromgate和togate,识别出数据值将从一个门的输出“流动”到下一个门的输入线。 对setNextPin的调用对于建立连接非常重要(参见Listing 13)。 我们需要将此方法添加到我们的门类中,以便每个togate可以为连接选择正确的输入行。
Listing 12
class Connector:def __init__(self, fgate, tgate):self.fromgate = fgateself.togate = tgatetgate.setNextPin(self)def getFrom(self):return self.fromgatedef getTo(self):return self.togate
在BinaryGate类中,对于具有两条可能输入线的门,连接器必须仅连接到一条线。 如果它们都可用,我们将默认选择pinA。 如果pinA已经连接,那么我们将选择pinB。 无法连接到没有可用输入线的门。
Listing 13
def setNextPin(self,source):if self.pinA == None:self.pinA = sourceelse:if self.pinB == None:self.pinB = sourceelse:raise RuntimeError("Error: NO EMPTY PINS")
现在可以从两个位置获取输入:外部,如前所述,以及连接到该输入线的门的输出。 这需要更改getPinA和getPinB方法(参见Listing 14)。 如果输入行没有连接到任何内容(空),则像以前一样向外部询问用户。 但是,如果存在连接,则访问连接并检索fromgate的输出值。 这反过来导致该门处理其逻辑。 这一直持续到所有输入都可用并且最终输出值成为所讨论的门的所需输入。 从某种意义上说,电路向后工作以找到最终产生输出所需的输入。
Listing 14
def getPinA(self):if self.pinA == None:return input("Enter Pin A input for gate " + self.getName()+"-->")else:return self.pinA.getFrom().getOutput()
以下片段构建了本节前面所示的电路:
>>> g1 = AndGate("G1")>>> g2 = AndGate("G2")>>> g3 = OrGate("G3")>>> g4 = NotGate("G4")>>> c1 = Connector(g1,g3)>>> c2 = Connector(g2,g3)>>> c3 = Connector(g3,g4)
两个与门(g1和g2)的输出连接到或门(g3),输出连接到非门(g4)。 非门的输出是整个电路的输出。 例如:
>>> g4.getOutput()Pin A input for gate G1-->0Pin B input for gate G1-->1Pin A input for gate G2-->1Pin B input for gate G2-->10
使用ActiveCode 4自己尝试一下:
ActiveCode 4
class LogicGate:def __init__(self,n):self.name = nself.output = Nonedef getName(self):return self.namedef getOutput(self):self.output = self.performGateLogic()return self.outputclass BinaryGate(LogicGate):def __init__(self,n):LogicGate.__init__(self,n)self.pinA = Noneself.pinB = Nonedef getPinA(self):if self.pinA == None:return int(input("Enter Pin A input for gate "+self.getName()+"-->"))else:return self.pinA.getFrom().getOutput()def getPinB(self):if self.pinB == None:return int(input("Enter Pin B input for gate "+self.getName()+"-->"))else:return self.pinB.getFrom().getOutput()def setNextPin(self,source):if self.pinA == None:self.pinA = sourceelse:if self.pinB == None:self.pinB = sourceelse:print("Cannot Connect: NO EMPTY PINS on this gate")class AndGate(BinaryGate):def __init__(self,n):BinaryGate.__init__(self,n)def performGateLogic(self):a = self.getPinA()b = self.getPinB()if a==1 and b==1:return 1else:return 0class OrGate(BinaryGate):def __init__(self,n):BinaryGate.__init__(self,n)def performGateLogic(self):a = self.getPinA()b = self.getPinB()if a ==1 or b==1:return 1else:return 0class UnaryGate(LogicGate):def __init__(self,n):LogicGate.__init__(self,n)self.pin = Nonedef getPin(self):if self.pin == None:return int(input("Enter Pin input for gate "+self.getName()+"-->"))else:return self.pin.getFrom().getOutput()def setNextPin(self,source):if self.pin == None:self.pin = sourceelse:print("Cannot Connect: NO EMPTY PINS on this gate")class NotGate(UnaryGate):def __init__(self,n):UnaryGate.__init__(self,n)def performGateLogic(self):if self.getPin():return 0else:return 1class Connector:def __init__(self, fgate, tgate):self.fromgate = fgateself.togate = tgatetgate.setNextPin(self)def getFrom(self):return self.fromgatedef getTo(self):return self.togatedef main():g1 = AndGate("G1")g2 = AndGate("G2")g3 = OrGate("G3")g4 = NotGate("G4")c1 = Connector(g1,g3)c2 = Connector(g2,g3)c3 = Connector(g3,g4)print(g4.getOutput())main()
自我检测
创建两个新的门类,一个名为NorGate,另一个名为NandGate。 NandGates像AndGates一样工作,它没有附加到输出。 NorGates工作的湖OrGates没有附加到输出。
创建一系列门,证明以下等式NOT(( A and B) or (C and D))与NOT( A and B ) and NOT (C and D)相同。 确保在模拟中使用一些新的门。
