3.6.简单括号匹配

我们现在把注意力转向使用栈解决真正的计算机问题。你会这么写算术表达式

(5+6)*(7+8)/(4+3)

其中括号用于命令操作的执行。你可能也有一些语言的经验，如 Lisp 的构造

(defun square(n)
     (* n n))

这段代码定义了一个名为 square 的函数，它将返回参数的 n 的平方。 Lisp 使用大量的圆括号是臭名昭著的。

在这两个例子中，括号必须以匹配的方式出现。括号匹配意味着每个开始符号具有相应的结束符号，并且括号能被正确嵌套。考虑下面正确匹配的括号字符串：

(()()()())
(((())))
(()((())()))

对比那些不匹配的括号：

((((((())
()))
(()()(()

区分括号是否匹配的能力是识别很多编程语言结构的重要部分。具有挑战的是如何编写一个算法，能够从左到右读取一串符号，并决定符号是否平衡。为了解决这个问题，我们需要做一个重要的观察。从左到右处理符号时，最近开始符号必须与下一个关闭符号相匹配(见 Figure 4)。此外，处理的第一个开始符号必须等待直到其匹配最后一个符号。结束符号以相反的顺序匹配开始符号。他们从内到外匹配。这是一个可以用栈解决问题的线索。

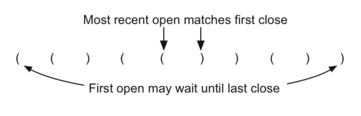
Figure 4

一旦你认为栈是保存括号的恰当的数据结构，算法是很直接的。从空栈开始，从左到右处理括号字符串。如果一个符号是一个开始符号，将其作为一个信号，对应的结束符号稍后会出现。另一方面，如果符号是结束符号，弹出栈，只要弹出栈的开始符号可以匹配每个结束符号，则括号保持匹配状态。如果任何时候栈上没有出现符合开始符号的结束符号，则字符串不匹配。最后，当所有符号都被处理后，栈应该是空的。实现此算法的 Python 代码见 ActiveCode 1。

from pythonds.basic.stack import Stack
def parChecker(symbolString):
    s = Stack()
    balanced = True
    index = 0
    while index < len(symbolString) and balanced:
        symbol = symbolString[index]
        if symbol == "(":
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced = False
            else:
                s.pop()
        index = index + 1
    if balanced and s.isEmpty():
        return True
    else:
        return False
print(parChecker('((()))'))
print(parChecker('(()'))

ActiveCode 1