4.3.计算整数列表和

我们将以一个简单的问题开始，你已经知道如何不使用递归解决。 假设你想计算整数列表的总和，例如：[1,3,5,7,9]。 计算总和的迭代函数见ActiveCode 1。函数使用累加器变量（theSum）来计算列表中所有整数的和，从 0 开始，加上列表中的每个数字。

def listsum(numList):
    theSum = 0
    for i in numList:
        theSum = theSum + i
    return theSum
print(listsum([1,3,5,7,9]))

Activecode 1

假设没有 while 循环或 for 循环。你将如何计算整数列表的总和？如果你是一个数学家，你可能开始回忆加法是一个函数，这个函数定义了两个整数类型的参数。故将列表和问题从加一个列表重新定义为加一对整数，我们可以把列表重写为一个完全括号表达式。如下所示：

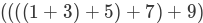
我们也可以把表达式用另一种方式括起来

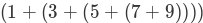
注意，最内层的括号（7 + 9）我们可以没有循环或任何特殊的结构来解决它。 事实上，我们可以使用以下的简化序列来计算最终的和。

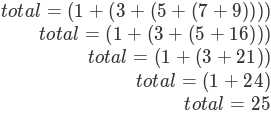
我们如何能把这个想法变成一个 Python 程序？ 首先，让我们以 Python 列表的形式重述求和问题。 我们可以说列表 numList 的和是列表的第一个元素numList[0] 和列表其余部分numList[1:] 之和的总和。 以函数形式表述：

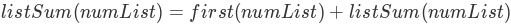
在这个方程式中，first(numList) 返回列表的第一个元素，rest(numList) 返回除第一个元素之外的所有元素列表。这很容易在 Python 中表示，如 ActiveCode 2 中所示。

def listsum(numList):
   if len(numList) == 1:
        return numList[0]
   else:
        return numList[0] + listsum(numList[1:])
print(listsum([1,3,5,7,9]))

Active code 2

在这个清单中有几个关键地方。 首先，在第 2 行，我们检查列表是否为一个元素。这个检查是至关重要的，是我们的函数的转折子句。 长度为 1 的列表和是微不足道的; 它只是列表中的数字。 第二，在第 5 行函数调用自己！ 这就是我们称 listum 算法递归的原因。递归函数是调用自身的函数。

Figure 1 展示了对列表[1,3,5,7,9] 求和所需的一系列递归调用。 你应该把这一系列的调用想象成一系列的简化。 每次我们进行递归调用时，我们都会解决一个较小的问题，直到达到问题不能减小的程度。

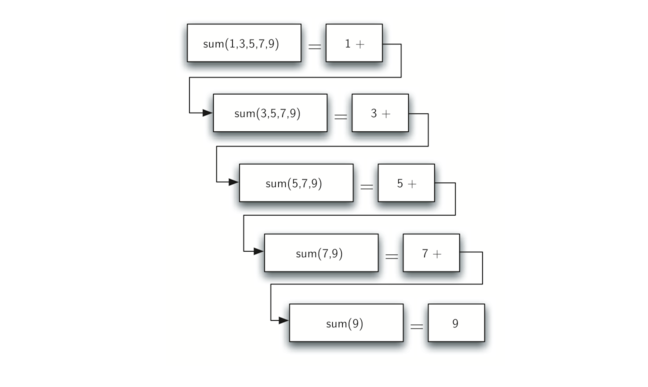
Figure 1

当我们到达简单问题的点，我们开始拼凑每个小问题的答案，直到初始问题解决。Figure 2 展示了在 listsum 通过一系列调用返回的过程中执行的 add 操作。当 listsum 从最顶层返回时，我们就有了整个问题的答案。

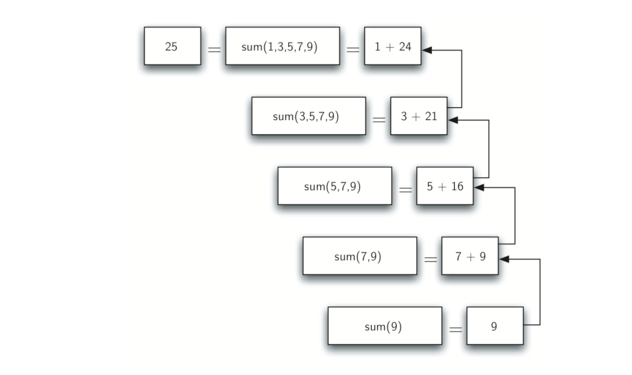
Figure 2