6.13.查找树实现

6.13.查找树实现

二叉搜索树依赖于在左子树中找到的键小于父节点的属性，并且在右子树中找到的键大于父代。我们将这个称为 bst属性。当我们如上所述实现 Map 接口时，bst 属性将指导我们的实现。 Figure 1说明了二叉搜索树的此属性，展示了没有任何关联值的键。请注意，该属性适用于每个父级和子级。左子树中的所有键小于根中的键。右子树中的所有键都大于根。

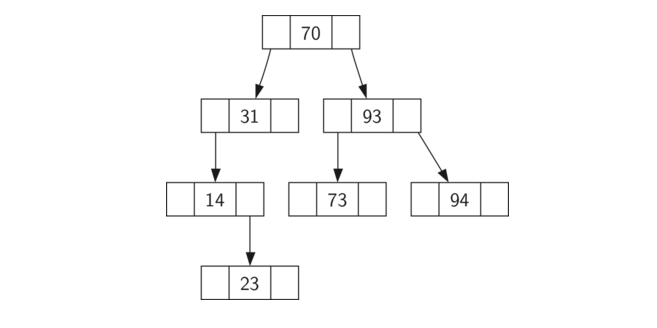
6.13.查找树实现.figure1

Figure1

现在你知道什么是二叉搜索树，我们将看看如何构造二叉搜索树。Figure 1中的搜索树表示在按照所示的顺序插入以下键之后存在的节点：70,31,93,94,14,23,73。因为 70 是插入树中的第一个键，它是根。接下来，31 小于 70，所以它成为 70 的左孩子。接下来，93 大于 70，所以它成为 70 的右孩子。现在我们有两层的树填充，所以下一个键 94 ，因为 94 大于70 和 93，它成为 93 的右孩子。类似地，14 小于 70 和 31，所以它变成 31 的左孩子。23 也小于 31，所以它必须在左子树 31 中。但是，它大于14，所以它成为 14 的右孩子。

为了实现二叉搜索树，我们将使用类似于我们用于实现链表的节点和引用方法，以及表达式树。但是，因为我们必须能够创建和使用一个空的二叉搜索树，我们的实现将使用两个类。第一个类称为 BinarySearchTree，第二个类称为TreeNode。 BinarySearchTree 类具有对作为二叉搜索树的根的TreeNode 的引用。在大多数情况下，外部类中定义的外部方法只是检查树是否为空。如果树中有节点，请求只是传递到 BinarySearchTree 类中定义的私有方法，该方法以 root 作为参数。在树是空的或者我们想要删除树根的键的情况下，我们必须采取特殊的行动。 BinarySearchTree 类构造函数的代码以及一些其他杂项函数如Listing 1所示。

class BinarySearchTree:
    def __init__(self):
        self.root = None
        self.size = 0
    def length(self):
        return self.size
    def __len__(self):
        return self.size
    def __iter__(self):
        return self.root.__iter__()

Listing 1

TreeNode 类提供了许多辅助函数，使得在 BinarySearchTree 类方法中完成的工作更容易。 TreeNode 的构造函数以及这些辅助函数如 Listing 2所示。你可以在列表中看到许多辅助函数根据自己的位置将节点分类为子节点（左或右）和节点具有的子节点类型。 TreeNode 类还将显式地跟踪父节点作为每个节点的属性。当我们讨论 del 操作符的实现时，你会看到为什么这很重要。

Listing 2 中 TreeNode 另一个有趣的方面是我们使用 Python 的可选参数。可选参数使我们能够在几种不同的情况下轻松创建 TreeNode 。有时我们想要构造一个已经同时具有父和子的新 TreeNode 。对于现有的父和子，我们可以传递父和子作为参数。在其他时候，我们将使用键值对创建一个TreeNode，我们不会为父或子传递任何参数。在这种情况下，将使用可选参数的默认值。

class TreeNode:
   def __init__(self,key,val,left=None,right=None,
                                       parent=None):
        self.key = key
        self.payload = val
        self.leftChild = left
        self.rightChild = right
        self.parent = parent
    def hasLeftChild(self):
        return self.leftChild
    def hasRightChild(self):
        return self.rightChild
    def isLeftChild(self):
        return self.parent and self.parent.leftChild == self
    def isRightChild(self):
        return self.parent and self.parent.rightChild == self
    def isRoot(self):
        return not self.parent
    def isLeaf(self):
        return not (self.rightChild or self.leftChild)
    def hasAnyChildren(self):
        return self.rightChild or self.leftChild
    def hasBothChildren(self):
        return self.rightChild and self.leftChild
    def replaceNodeData(self,key,value,lc,rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.hasLeftChild():
            self.leftChild.parent = self
        if self.hasRightChild():
            self.rightChild.parent = self

Listing 2

现在我们有了 BinarySearchTree shell 和 TreeNode，现在是时候编写 put 方法，这将允许我们构建二叉搜索树。 put 方法是BinarySearchTree 类的一个方法。此方法将检查树是否已具有根。如果没有根，那么 put 将创建一个新的 TreeNode 并将其做为树的根。如果根节点已经就位，则 put 调用私有递归辅助函数 _put 根据以下算法搜索树：

从树的根开始，搜索二叉树，将新键与当前节点中的键进行比较。如果新键小于当前节点，则搜索左子树。如果新键大于当前节点，则搜索右子树。
当没有左（或右）孩子要搜索时，我们在树中找到应该建立新节点的位置。
要向树中添加节点，请创建一个新的 TreeNode 对象，并将对象插入到上一步发现的节点。Listing 3 展示了在树中插入一个新节点的 Python 代码。_put 函数按照上述步骤递归编写。请注意，当一个新的子节点插入到树中时，currentNode 将作为父节点传递给新的树节点。

我们实现插入的一个重要问题是重复的键不能正确处理。当我们的树被实现时，重复键将在具有原始键的节点的右子树中创建具有相同键值的新节点。这样做的结果是，具有新键的节点将永远不会在搜索期间被找到。处理插入重复键的更好方法是将新键相关联的值替换旧值。我们将修复这个bug作为练习。

def put(self,key,val):
    if self.root:
        self._put(key,val,self.root)
    else:
        self.root = TreeNode(key,val)
    self.size = self.size + 1
def _put(self,key,val,currentNode):
    if key < currentNode.key:
        if currentNode.hasLeftChild():
               self._put(key,val,currentNode.leftChild)
        else:
               currentNode.leftChild = TreeNode(key,val,parent=currentNode)
    else:
        if currentNode.hasRightChild():
               self._put(key,val,currentNode.rightChild)
        else:
               currentNode.rightChild = TreeNode(key,val,parent=currentNode)

Listing 3

当 put 方法定义后，我们可以通过使用 setitem 方法调用（参见 Listing 4 ）put 方法来重载赋值的 [] 运算符。这使得我们可以编写像myZipTree['Plymouth'] = 55446 这样的 Python 语句，就像 Python 字典一样。

def __setitem__(self,k,v):
    self.put(k,v)

Listing 4

Figure 2 展示了用于将新节点插入二叉搜索树的过程。浅阴影的节点指示在插入过程期间访问的节点。

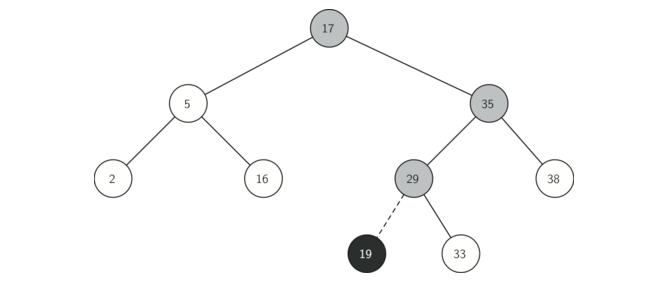
6.13.查找树实现.figure2

Figure 2

一旦树被构造，下一个任务是实现对给定键的值的检索。get 方法比 put 方法更容易，因为它只是递归地搜索树，直到它到达不匹配的叶节点或找到匹配的键。当找到匹配的键时，返回存储在节点的有效载荷中的值。

Listing 5 展示了 get ，get 和 _getitem 的代码。 _get 方法中的搜索代码使用和 _put 相同的逻辑来选择左或右子节点。请注意，_get 方法返回一个 TreeNode ，这允许 _get 用作其他BinarySearchTree 方法的一个灵活的辅助方法，可能需要利用除了有效载荷之外的 TreeNode 的其他数据。

通过实现 getitem 方法，我们可以编写一个类似于访问字典的 Python 语句，而实际上我们使用的是二叉搜索树，例如 z = myZipTree ['Fargo'] 。正如你所看到的，所有的 getitem 方法都是调用get 。

def get(self,key):
    if self.root:
        res = self._get(key,self.root)
        if res:
               return res.payload
        else:
               return None
    else:
        return None
def _get(self,key,currentNode):
    if not currentNode:
        return None
    elif currentNode.key == key:
        return currentNode
    elif key < currentNode.key:
        return self._get(key,currentNode.leftChild)
    else:
        return self._get(key,currentNode.rightChild)
def __getitem__(self,key):
    return self.get(key)

Listing 5

使用 get ，我们可以通过为 BinarySearchTree 写一个contains 方法来实现 in 操作。 contains 方法将简单地调用 get 并在 get 返回值时返回 True，如果返回 None 则返回 False。 contains 的代码如Listing 6所示。

def __contains__(self,key):
    if self._get(key,self.root):
        return True
    else:
        return False

Listing 6

回想一下，contains 重载了 in 操作符，允许我们写出如下语句：

if 'Northfield' in myZipTree:
    print("oom ya ya")

最后，我们将注意力转向二叉搜索树中最具挑战性的方法，删除一个键（参见 Listing 7）。第一个任务是通过搜索树来找到要删除的节点。如果树具有多个节点，我们使用 _get 方法搜索以找到需要删除的 TreeNode。如果树只有一个节点，这意味着我们删除树的根，但是我们仍然必须检查以确保根的键匹配要删除的键。在任一情况下，如果未找到键，del 操作符将引发错误。

def delete(self,key):
   if self.size > 1:
      nodeToRemove = self._get(key,self.root)
      if nodeToRemove:
          self.remove(nodeToRemove)
          self.size = self.size-1
      else:
          raise KeyError('Error, key not in tree')
   elif self.size == 1 and self.root.key == key:
      self.root = None
      self.size = self.size - 1
   else:
      raise KeyError('Error, key not in tree')
def __delitem__(self,key):
    self.delete(key)

Listing 7

一旦我们找到了我们要删除的键的节点，我们必须考虑三种情况：

要删除的节点没有子节点（参见Figure 3）。
要删除的节点只有一个子节点（见Figure 4）。
要删除的节点有两个子节点（见Figure 5）。第一种情况很简单（见 Listing 8）。如果当前节点没有子节点，我们需要做的是删除节点并删除对父节点中该节点的引用。此处的代码如下所示。

if currentNode.isLeaf():
    if currentNode == currentNode.parent.leftChild:
        currentNode.parent.leftChild = None
    else:
        currentNode.parent.rightChild = None

Listing 8

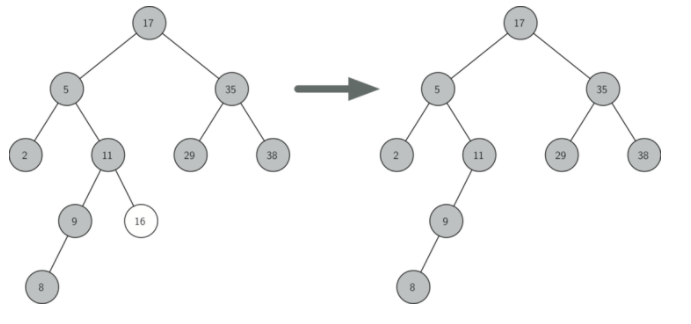
6.13.查找树实现.figure3

Figure 3

第二种情况只是稍微复杂一点（见 Listing 9）。如果一个节点只有一个孩子，那么我们可以简单地促进孩子取代其父。此案例的代码展示在下一个列表中。当你看这个代码，你会看到有六种情况要考虑。由于这些情况相对于左孩子或右孩子对称，我们将仅讨论当前节点具有左孩子的情况。决策如下：

如果当前节点是左子节点，则我们只需要更新左子节点的父引用以指向当前节点的父节点，然后更新父节点的左子节点引用以指向当前节点的左子节点。
如果当前节点是右子节点，则我们只需要更新左子节点的父引用以指向当前节点的父节点，然后更新父节点的右子节点引用以指向当前节点的左子节点。
如果当前节点没有父级，则它是根。在这种情况下，我们将通过在根上调用replaceNodeData 方法来替换 key，payload，leftChild 和 rightChild 数据。

else: # this node has one child
   if currentNode.hasLeftChild():
      if currentNode.isLeftChild():
          currentNode.leftChild.parent = currentNode.parent
          currentNode.parent.leftChild = currentNode.leftChild
      elif currentNode.isRightChild():
          currentNode.leftChild.parent = currentNode.parent
          currentNode.parent.rightChild = currentNode.leftChild
      else:
          currentNode.replaceNodeData(currentNode.leftChild.key,
                             currentNode.leftChild.payload,
                             currentNode.leftChild.leftChild,
                             currentNode.leftChild.rightChild)
   else:
      if currentNode.isLeftChild():
          currentNode.rightChild.parent = currentNode.parent
          currentNode.parent.leftChild = currentNode.rightChild
      elif currentNode.isRightChild():
          currentNode.rightChild.parent = currentNode.parent
          currentNode.parent.rightChild = currentNode.rightChild
      else:
          currentNode.replaceNodeData(currentNode.rightChild.key,
                             currentNode.rightChild.payload,
                             currentNode.rightChild.leftChild,
                             currentNode.rightChild.rightChild)

Listing 9

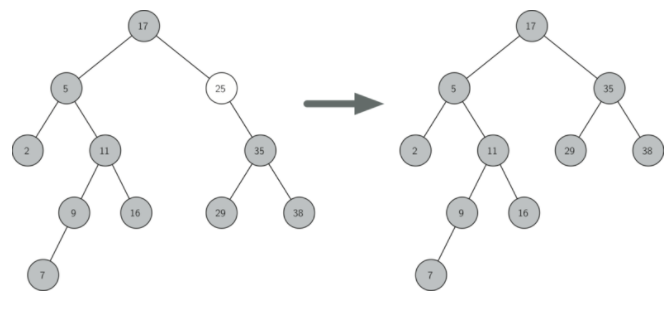
6.13.查找树实现.figure4

Figure 4

第三种情况是最难处理的情况（见Listing 10）。如果一个节点有两个孩子，那么我们不太可能简单地提升其中一个节点来占据节点的位置。然而，我们可以在树中搜索可用于替换被调度删除的节点的节点。我们需要的是一个节点，它将保留现有的左和右子树的二叉搜索树关系。执行此操作的节点是树中具有次最大键的节点。我们将这个节点称为后继节点，我们将看一种方法来很快找到后继节点。继承节点保证没有多于一个孩子，所以我们知道使用已经实现的两种情况删除它。一旦删除了后继，我们只需将它放在树中，代替要删除的节点。

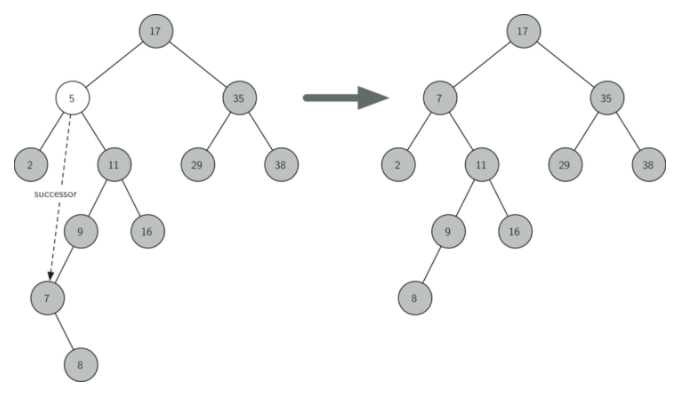
6.13.查找树实现.figure5

Figure 5

处理第三种情况的代码展示在下一个列表中。注意，我们使用辅助方法findSuccessor 和 findMin 来找到后继。要删除后继，我们使用spliceOut 方法。我们使用 spliceOut 的原因是它直接找到我们想要拼接的节点，并做出正确的更改。我们可以递归调用删除，但是我们将浪费时间重新搜索关键节点。

elif currentNode.hasBothChildren(): #interior
        succ = currentNode.findSuccessor()
        succ.spliceOut()
        currentNode.key = succ.key
        currentNode.payload = succ.payload

Listing 10

找到后继的代码如下所示（见 Listing 11），是 TreeNode 类的一个方法。此代码利用二叉搜索树的相同属性，采用中序遍历从最小到最大打印树中的节点。在寻找接班人时，有三种情况需要考虑：

如果节点有右子节点，则后继节点是右子树中的最小的键。
如果节点没有右子节点并且是父节点的左子节点，则父节点是后继节点。
如果节点是其父节点的右子节点，并且它本身没有右子节点，则此节点的后继节点是其父节点的后继节点，不包括此节点。第一个条件是对于我们从二叉搜索树中删除节点时唯一重要的条件。但是，findSuccessor 方法具有其他用法，我们将在本章结尾的练习中介绍。

调用 findMin 方法来查找子树中的最小键。你应该说服自己，任何二叉搜索树中的最小值键是树的最左子节点。因此，findMin 方法简单地循环子树的每个节点中的 leftChild 引用，直到它到达没有左子节点的节点。

def findSuccessor(self):
    succ = None
    if self.hasRightChild():
        succ = self.rightChild.findMin()
    else:
        if self.parent:
               if self.isLeftChild():
                   succ = self.parent
               else:
                   self.parent.rightChild = None
                   succ = self.parent.findSuccessor()
                   self.parent.rightChild = self
    return succ
def findMin(self):
    current = self
    while current.hasLeftChild():
        current = current.leftChild
    return current
def spliceOut(self):
    if self.isLeaf():
        if self.isLeftChild():
               self.parent.leftChild = None
        else:
               self.parent.rightChild = None
    elif self.hasAnyChildren():
        if self.hasLeftChild():
               if self.isLeftChild():
                  self.parent.leftChild = self.leftChild
               else:
                  self.parent.rightChild = self.leftChild
               self.leftChild.parent = self.parent
        else:
               if self.isLeftChild():
                  self.parent.leftChild = self.rightChild
               else:
                  self.parent.rightChild = self.rightChild
               self.rightChild.parent = self.parent

Listing 11

我们需要查看二叉搜索树的最后一个接口方法。假设我们想要按中序遍历树中的所有键。我们肯定用字典做，为什么不是树？你已经知道如何使用中序遍历算法按顺序遍历二叉树。然而，编写迭代器需要更多的工作，因为迭代器在每次调用迭代器时只返回一个节点。

Python 为我们提供了一个非常强大的函数，在创建迭代器时使用。该函数称为yield 。 yield 类似于 return，因为它向调用者返回一个值。然而，yield 采取冻结函数状态的附加步骤，使得下一次调用函数时，它从其早先停止的确切点继续执行。创建可以迭代的对象的函数称为生成函数。

二叉树的 inorder 迭代器的代码展示在下一个列表中。仔细看看这段代码;乍一看，你可能认为代码不是递归的。但是，请记住，iter 覆盖 for x in操作，因此它是递归的！因为它是在 TreeNode 实例上递归的，所以iter 方法在 TreeNode 类中定义。

def __iter__(self):
   if self:
      if self.hasLeftChild():
             for elem in self.leftChild:
                yield elem
      yield self.key
      if self.hasRightChild():
             for elem in self.rightChild:
                yield elem

此时，你可能需要下载包含完整版本的 BinarySearchTree 和 TreeNode 类的整个文件。

class TreeNode:
    def __init__(self,key,val,left=None,right=None,parent=None):
        self.key = key
        self.payload = val
        self.leftChild = left
        self.rightChild = right
        self.parent = parent
    def hasLeftChild(self):
        return self.leftChild
    def hasRightChild(self):
        return self.rightChild
    def isLeftChild(self):
        return self.parent and self.parent.leftChild == self
    def isRightChild(self):
        return self.parent and self.parent.rightChild == self
    def isRoot(self):
        return not self.parent
    def isLeaf(self):
        return not (self.rightChild or self.leftChild)
    def hasAnyChildren(self):
        return self.rightChild or self.leftChild
    def hasBothChildren(self):
        return self.rightChild and self.leftChild
    def replaceNodeData(self,key,value,lc,rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.hasLeftChild():
            self.leftChild.parent = self
        if self.hasRightChild():
            self.rightChild.parent = self
class BinarySearchTree:
    def __init__(self):
        self.root = None
        self.size = 0
    def length(self):
        return self.size
    def __len__(self):
        return self.size
    def put(self,key,val):
        if self.root:
            self._put(key,val,self.root)
        else:
            self.root = TreeNode(key,val)
        self.size = self.size + 1
    def _put(self,key,val,currentNode):
        if key < currentNode.key:
            if currentNode.hasLeftChild():
                   self._put(key,val,currentNode.leftChild)
            else:
                   currentNode.leftChild = TreeNode(key,val,parent=currentNode)
        else:
            if currentNode.hasRightChild():
                   self._put(key,val,currentNode.rightChild)
            else:
                   currentNode.rightChild = TreeNode(key,val,parent=currentNode)
    def __setitem__(self,k,v):
       self.put(k,v)
    def get(self,key):
       if self.root:
           res = self._get(key,self.root)
           if res:
                  return res.payload
           else:
                  return None
       else:
           return None
    def _get(self,key,currentNode):
       if not currentNode:
           return None
       elif currentNode.key == key:
           return currentNode
       elif key < currentNode.key:
           return self._get(key,currentNode.leftChild)
       else:
           return self._get(key,currentNode.rightChild)
    def __getitem__(self,key):
       return self.get(key)
    def __contains__(self,key):
       if self._get(key,self.root):
           return True
       else:
           return False
    def delete(self,key):
      if self.size > 1:
         nodeToRemove = self._get(key,self.root)
         if nodeToRemove:
             self.remove(nodeToRemove)
             self.size = self.size-1
         else:
             raise KeyError('Error, key not in tree')
      elif self.size == 1 and self.root.key == key:
         self.root = None
         self.size = self.size - 1
      else:
         raise KeyError('Error, key not in tree')
    def __delitem__(self,key):
       self.delete(key)
    def spliceOut(self):
       if self.isLeaf():
           if self.isLeftChild():
                  self.parent.leftChild = None
           else:
                  self.parent.rightChild = None
       elif self.hasAnyChildren():
           if self.hasLeftChild():
                  if self.isLeftChild():
                     self.parent.leftChild = self.leftChild
                  else:
                     self.parent.rightChild = self.leftChild
                  self.leftChild.parent = self.parent
           else:
                  if self.isLeftChild():
                     self.parent.leftChild = self.rightChild
                  else:
                     self.parent.rightChild = self.rightChild
                  self.rightChild.parent = self.parent
    def findSuccessor(self):
      succ = None
      if self.hasRightChild():
          succ = self.rightChild.findMin()
      else:
          if self.parent:
                 if self.isLeftChild():
                     succ = self.parent
                 else:
                     self.parent.rightChild = None
                     succ = self.parent.findSuccessor()
                     self.parent.rightChild = self
      return succ
    def findMin(self):
      current = self
      while current.hasLeftChild():
          current = current.leftChild
      return current
    def remove(self,currentNode):
         if currentNode.isLeaf(): #leaf
           if currentNode == currentNode.parent.leftChild:
               currentNode.parent.leftChild = None
           else:
               currentNode.parent.rightChild = None
         elif currentNode.hasBothChildren(): #interior
           succ = currentNode.findSuccessor()
           succ.spliceOut()
           currentNode.key = succ.key
           currentNode.payload = succ.payload
         else: # this node has one child
           if currentNode.hasLeftChild():
             if currentNode.isLeftChild():
                 currentNode.leftChild.parent = currentNode.parent
                 currentNode.parent.leftChild = currentNode.leftChild
             elif currentNode.isRightChild():
                 currentNode.leftChild.parent = currentNode.parent
                 currentNode.parent.rightChild = currentNode.leftChild
             else:
                 currentNode.replaceNodeData(currentNode.leftChild.key,
                                    currentNode.leftChild.payload,
                                    currentNode.leftChild.leftChild,
                                    currentNode.leftChild.rightChild)
           else:
             if currentNode.isLeftChild():
                 currentNode.rightChild.parent = currentNode.parent
                 currentNode.parent.leftChild = currentNode.rightChild
             elif currentNode.isRightChild():
                 currentNode.rightChild.parent = currentNode.parent
                 currentNode.parent.rightChild = currentNode.rightChild
             else:
                 currentNode.replaceNodeData(currentNode.rightChild.key,
                                    currentNode.rightChild.payload,
                                    currentNode.rightChild.leftChild,
                                    currentNode.rightChild.rightChild)
mytree = BinarySearchTree()
mytree[3]="red"
mytree[4]="blue"
mytree[6]="yellow"
mytree[2]="at"
print(mytree[6])
print(mytree[2])