- 6.5.节点表示
6.5.节点表示
我们的第二种表示树的方法使用节点和引用。在这种情况下,我们将定义一个具有根值属性的类,以及左和右子树。 由于这个表示更接近于面向对象的编程范例,我们将继续使用这个表示法用于本章的剩余部分。
使用节点和引用,我们认为树结构类似于 Figure 2 所示。
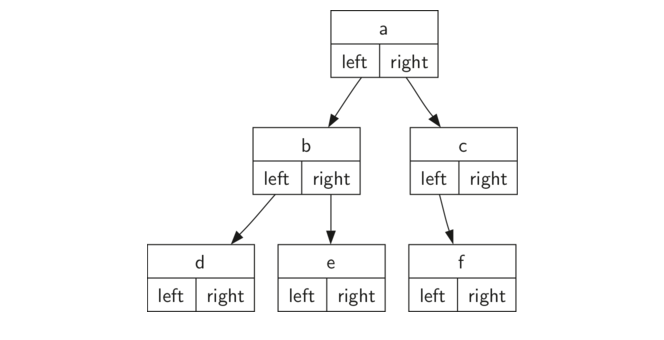
Figure 2
我们将从节点和引用方法的一个简单的类定义开始,如 Listing 4 所示。要记住这个表示重要的事情是 left 和 right 的属性将成为对 BinaryTree 类的其他实例的引用。 例如,当我们在树中插入一个新的左子节点时,我们创建另一个 BinaryTree 实例,并在根节点中修改self.leftChild 来引用新树节点。
class BinaryTree:def __init__(self,rootObj):self.key = rootObjself.leftChild = Noneself.rightChild = None
Listing 4
请注意,在 Listing 4 中,构造函数希望获取某种对象存储在根中。 就像你可以在列表中存储任何你喜欢的对象一样,树的根对象可以是对任何对象的引用。 对于我们的先前示例,我们将存储节点的名称作为根值。使用节点和引用来表示 Figure 2 中的树,我们将创建 BinaryTree 类的六个实例。
接下来,我们来看看需要构建超出根节点的树的函数。要向树中添加一个左子树,我们将创建一个新的二叉树对象,并设置根的左边属性来引用这个新对象。 insertLeft 的代码如 Listing 5所示。
def insertLeft(self,newNode):if self.leftChild == None:self.leftChild = BinaryTree(newNode)else:t = BinaryTree(newNode)t.leftChild = self.leftChildself.leftChild = t
Listing 5
我们必须考虑两种插入情况。 第一种情况的特征没有现有左孩子的节点。当没有左孩子时,只需向树中添加一个节点。 第二种情况的特征在于具有现有左孩子的节点。在第二种情况下,我们插入一个节点并将现有的子节点放到树中的下一个层。第二种情况由 Listing 5 第 4 行的 else 语句处理。
insertRight 的代码必须考虑一组对称的情况。没有右孩子,或者我们在根和现有右孩子之间插入节点。 插入代码如 Listing 6 所示。
def insertRight(self,newNode):if self.rightChild == None:self.rightChild = BinaryTree(newNode)else:t = BinaryTree(newNode)t.rightChild = self.rightChildself.rightChild = t
Listing 6
为了完成一个简单二叉树数据结构的定义,我们将实现获取 左和右孩子(见 Listing 7 )以及根值的方法。
def getRightChild(self):return self.rightChilddef getLeftChild(self):return self.leftChilddef setRootVal(self,obj):self.key = objdef getRootVal(self):return self.key
Listing 7
现在我们有了创建和操作二叉树的所有部分,让我们使用它们来检查结构。 我们使用节点 a 作为根的简单树,并将节点 b 和 c 添加为子节点。 ActiveCode 1 创建树并查看存储在 key,left 和 right 中的一些值。注意,根的左和右孩子本身是 BinaryTree 类的不同实例。正如我们在对树的原始递归定义中所说的,这允许我们将二叉树的任何子项视为二叉树本身。
class BinaryTree:def __init__(self,rootObj):self.key = rootObjself.leftChild = Noneself.rightChild = Nonedef insertLeft(self,newNode):if self.leftChild == None:self.leftChild = BinaryTree(newNode)else:t = BinaryTree(newNode)t.leftChild = self.leftChildself.leftChild = tdef insertRight(self,newNode):if self.rightChild == None:self.rightChild = BinaryTree(newNode)else:t = BinaryTree(newNode)t.rightChild = self.rightChildself.rightChild = tdef getRightChild(self):return self.rightChilddef getLeftChild(self):return self.leftChilddef setRootVal(self,obj):self.key = objdef getRootVal(self):return self.keyr = BinaryTree('a')print(r.getRootVal())print(r.getLeftChild())r.insertLeft('b')print(r.getLeftChild())print(r.getLeftChild().getRootVal())r.insertRight('c')print(r.getRightChild())print(r.getRightChild().getRootVal())r.getRightChild().setRootVal('hello')print(r.getRightChild().getRootVal())
