15.1 隐马尔可夫模型(HMM)

隐马尔可夫模型（Hidden Markov Model，简称HMM）是结构最简单的一种贝叶斯网，在语音识别与自然语言处理领域上有着广泛的应用。HMM中的变量分为两组：状态变量与观测变量，其中状态变量一般是未知的，因此又称为“隐变量”，观测变量则是已知的输出值。在隐马尔可夫模型中，变量之间的依赖关系遵循如下两个规则：

1. 观测变量的取值仅依赖于状态变量；2. 下一个状态的取值仅依赖于当前状态，通俗来讲：现在决定未来，未来与过去无关，这就是著名的马尔可夫性。

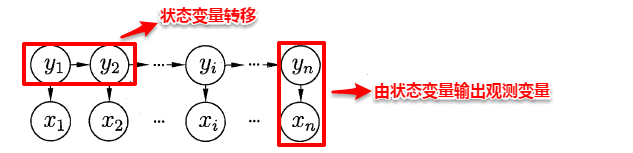
基于上述变量之间的依赖关系，我们很容易写出隐马尔可夫模型中所有变量的联合概率分布：

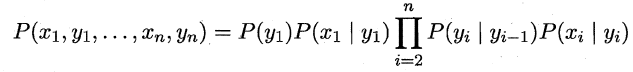
易知：欲确定一个HMM模型需要以下三组参数：

当确定了一个HMM模型的三个参数后，便按照下面的规则来生成观测值序列：

在实际应用中，HMM模型的发力点主要体现在下述三个问题上：

15.1.1 HMM评估问题

HMM评估问题指的是：给定了模型的三个参数与观测值序列，求该观测值序列出现的概率。例如：对于赌场问题，便可以依据骰子掷出的结果序列来计算该结果序列出现的可能性，若小概率的事件发生了则可认为赌场的骰子有作弊的可能。解决该问题使用的是前向算法，即步步为营，自底向上的方式逐步增加序列的长度，直到获得目标概率值。在前向算法中，定义了一个前向变量，即给定观察值序列且t时刻的状态为Si的概率：

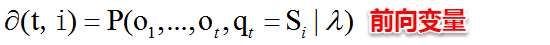
基于前向变量，很容易得到该问题的递推关系及终止条件：

因此可使用动态规划法，从最小的子问题开始，通过填表格的形式一步一步计算出目标结果。

15.1.2 HMM解码问题

HMM解码问题指的是：给定了模型的三个参数与观测值序列，求可能性最大的状态序列。例如：在语音识别问题中，人说话形成的数字信号对应着观测值序列，对应的具体文字则是状态序列，从数字信号转化为文字正是对应着根据观测值序列推断最有可能的状态值序列。解决该问题使用的是Viterbi算法，与前向算法十分类似地，Viterbi算法定义了一个Viterbi变量，也是采用动态规划的方法，自底向上逐步求解。

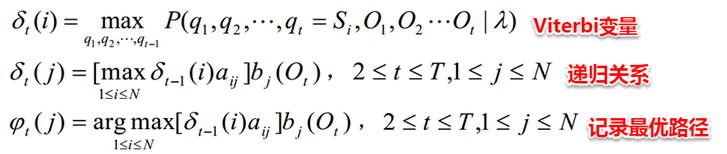
15.1.3 HMM学习问题

HMM学习问题指的是：给定观测值序列，如何调整模型的参数使得该序列出现的概率最大。这便转化成了机器学习问题，即从给定的观测值序列中学习出一个HMM模型，该问题正是EM算法的经典案例之一。其思想也十分简单：对于给定的观测值序列，如果我们能够按照该序列潜在的规律来调整模型的三个参数，则可以使得该序列出现的可能性最大。假设状态值序列也已知，则很容易计算出与该序列最契合的模型参数：

但一般状态值序列都是不可观测的，且即使给定观测值序列与模型参数，状态序列仍然遭遇组合爆炸。因此上面这种简单的统计方法就行不通了，若将状态值序列看作为隐变量，这时便可以考虑使用EM算法来对该问题进行求解：

【1】首先对HMM模型的三个参数进行随机初始化；【2】根据模型的参数与观测值序列，计算t时刻状态为i且t+1时刻状态为j的概率以及t时刻状态为i的概率。

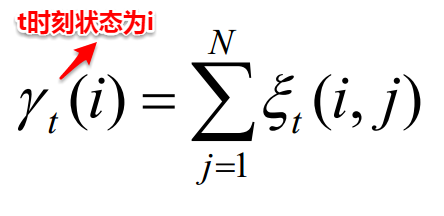
【3】接着便可以对模型的三个参数进行重新估计：

【4】重复步骤2-3，直至三个参数值收敛，便得到了最终的HMM模型。