6.5 软间隔支持向量机

前面的讨论中，我们主要解决了两个问题：当数据线性可分时，直接使用最大间隔的超平面划分；当数据线性不可分时，则通过核函数将数据映射到高维特征空间，使之线性可分。然而在现实问题中，对于某些情形还是很难处理，例如数据中有噪声的情形，噪声数据（outlier）本身就偏离了正常位置，但是在前面的SVM模型中，我们要求所有的样本数据都必须满足约束，如果不要这些噪声数据还好，当加入这些outlier后导致划分超平面被挤歪了，如下图所示，对支持向量机的泛化性能造成很大的影响。

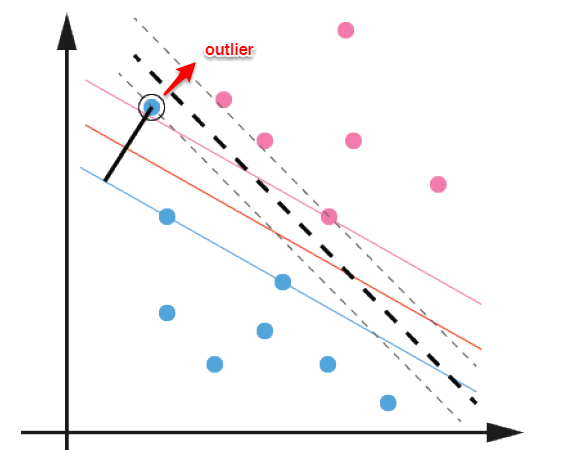
为了解决这一问题，我们需要允许某一些数据点不满足约束，即可以在一定程度上偏移超平面，同时使得不满足约束的数据点尽可能少，这便引出了“软间隔”支持向量机的概念

* 允许某些数据点不满足约束y(w'x+b)≥1；
* 同时又使得不满足约束的样本尽可能少。

这样优化目标变为：

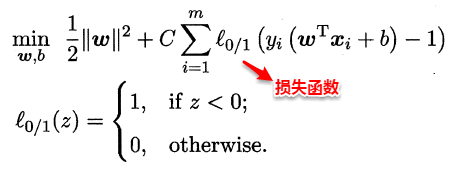
如同阶跃函数，0/1损失函数虽然表示效果最好，但是数学性质不佳。因此常用其它函数作为“替代损失函数”。

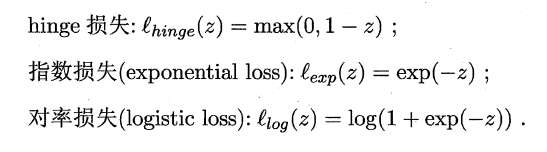
支持向量机中的损失函数为hinge损失，引入“松弛变量”，目标函数与约束条件可以写为：

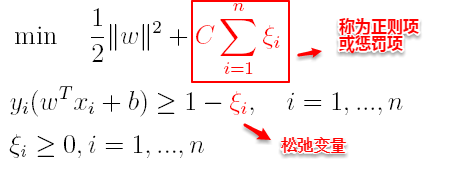
其中C为一个参数，控制着目标函数与新引入正则项之间的权重，这样显然每个样本数据都有一个对应的松弛变量，用以表示该样本不满足约束的程度，将新的目标函数转化为拉格朗日函数得到：

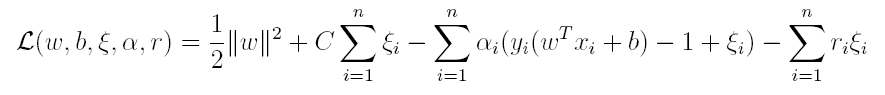
按照与之前相同的方法，先让L求关于w，b以及松弛变量的极小，再使用SMO求出α，有：

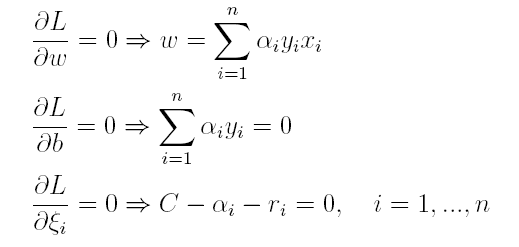
将w代入L化简，便得到其对偶问题：

将“软间隔”下产生的对偶问题与原对偶问题对比可以发现：新的对偶问题只是约束条件中的α多出了一个上限C，其它的完全相同，因此在引入核函数处理线性不可分问题时，便能使用与“硬间隔”支持向量机完全相同的方法。

——在此SVM就介绍完毕。