- 11.2. 数学基础
- 11.2.1. 线性代数
- 11.2.1.1. 向量
- 11.2.1.2. 矩阵
- 11.2.1.3. 运算
- 11.2.1.4. 范数
- 11.2.1.5. 特征向量和特征值
- 11.2.2. 微分
- 11.2.2.1. 导数和微分
- 11.2.2.2. 泰勒展开
- 11.2.2.3. 偏导数
- 11.2.2.4. 梯度
- 11.2.2.5. 海森矩阵
- 11.2.3. 概率
- 11.2.3.1. 条件概率
- 11.2.3.2. 期望
- 11.2.3.3. 均匀分布
- 11.2.4. 小结
- 11.2.5. 练习
- 11.2.1. 线性代数
11.2. 数学基础
本节总结了本书中涉及的有关线性代数、微分和概率的基础知识。为避免赘述本书未涉及的数学背景知识,本节中的少数定义稍有简化。
11.2.1. 线性代数
下面分别概括了向量、矩阵、运算、范数、特征向量和特征值的概念。
11.2.1.1. 向量
本书中的向量指的是列向量。一个
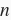 维向量
维向量
 的表达式可写成
的表达式可写成

其中
 是向量的元素。我们将各元素均为实数的
是向量的元素。我们将各元素均为实数的
 维向量
维向量
 记作
记作
 或
或
 。
。
11.2.1.2. 矩阵
一个
 行
行
 列矩阵的表达式可写成
列矩阵的表达式可写成

其中
 是矩阵
是矩阵
 中第
中第
 行第
行第
 列的元素(
列的元素(
 )。我们将各元素均为实数的
)。我们将各元素均为实数的
 行
行
 列矩阵
列矩阵
 记作
记作
 。不难发现,向量是特殊的矩阵。
。不难发现,向量是特殊的矩阵。
11.2.1.3. 运算
设
 维向量
维向量
 中的元素为
中的元素为
 ,
,
 维向量
维向量
 中的元素为
中的元素为
 。向量
。向量
 与
与
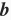 的点乘(内积)是一个标量:
的点乘(内积)是一个标量:

设两个
 行
行
 列矩阵
列矩阵

矩阵
 的转置是一个
的转置是一个
 行
行
 列矩阵,它的每一行其实是原矩阵的每一列:
列矩阵,它的每一行其实是原矩阵的每一列:

两个相同形状的矩阵的加法是将两个矩阵按元素做加法:

我们使用符号
 表示两个矩阵按元素做乘法的运算:
表示两个矩阵按元素做乘法的运算:

定义一个标量
 。标量与矩阵的乘法也是按元素做乘法的运算:
。标量与矩阵的乘法也是按元素做乘法的运算:

其他诸如标量与矩阵按元素相加、相除等运算与上式中的相乘运算类似。矩阵按元素开根号、取对数等运算也就是对矩阵每个元素开根号、取对数等,并得到和原矩阵形状相同的矩阵。
矩阵乘法和按元素的乘法不同。设
 为
为
 行
行
 列的矩阵,
列的矩阵,
 为
为
 行
行
 列的矩阵。两个矩阵相乘的结果
列的矩阵。两个矩阵相乘的结果

是一个
 行
行
 列的矩阵,其中第
列的矩阵,其中第
 行第
行第
 列(
列(
 )的元素为
)的元素为

11.2.1.4. 范数
设
 维向量
维向量
 中的元素为
中的元素为
 。向量
。向量
 的
的
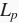 范数为
范数为

例如,
 的
的
 范数是该向量元素绝对值之和:
范数是该向量元素绝对值之和:

而
 的
的
 范数是该向量元素平方和的平方根:
范数是该向量元素平方和的平方根:

我们通常用
 指代
指代
 。
。
设
 是一个
是一个
 行
行
 列矩阵。矩阵
列矩阵。矩阵
 的Frobenius范数为该矩阵元素平方和的平方根:
的Frobenius范数为该矩阵元素平方和的平方根:

其中
 为矩阵
为矩阵
 在第
在第
 行第
行第
 列的元素。
列的元素。
11.2.1.5. 特征向量和特征值
对于一个
 行
行
 列的矩阵
列的矩阵
 ,假设有标量
,假设有标量
 和非零的
和非零的
 维向量
维向量
 使
使

那么
 是矩阵
是矩阵
 的一个特征向量,标量
的一个特征向量,标量
 是
是
 对应的特征值。
对应的特征值。
11.2.2. 微分
我们在这里简要介绍微分的一些基本概念和演算。
11.2.2.1. 导数和微分
假设函数
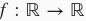 的输入和输出都是标量。函数
的输入和输出都是标量。函数
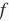 的导数
的导数
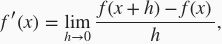
且假定该极限存在。给定
 ,其中
,其中
 和
和
 分别是函数
分别是函数
 的自变量和因变量。以下有关导数和微分的表达式等价:
的自变量和因变量。以下有关导数和微分的表达式等价:

其中符号
 和
和
 也叫微分运算符。常见的微分演算有
也叫微分运算符。常见的微分演算有
 (
(
 为常数)、
为常数)、
 (
(
 为常数)、
为常数)、
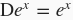 、
、
 等。
等。
如果函数
 和
和
 都可导,设
都可导,设
 为常数,那么
为常数,那么

如果
 和
和
 都是可导函数,依据链式法则,
都是可导函数,依据链式法则,

11.2.2.2. 泰勒展开
函数
 的泰勒展开式是
的泰勒展开式是

其中
 为函数
为函数
 的
的
 阶导数(求
阶导数(求
 次导数),
次导数),
 为
为
 的阶乘。假设
的阶乘。假设
 是一个足够小的数,如果将上式中
是一个足够小的数,如果将上式中
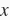 和
和
 分别替换成
分别替换成
 和
和
 ,可以得到
,可以得到

由于
 足够小,上式也可以简化成
足够小,上式也可以简化成

11.2.2.3. 偏导数
设
 为一个有
为一个有
 个自变量的函数,
个自变量的函数,
 ,它有关第
,它有关第
 个变量
个变量
 的偏导数为
的偏导数为

以下有关偏导数的表达式等价:
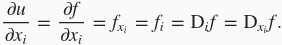
为了计算
 ,只需将
,只需将
 视为常数并求
视为常数并求
 有关
有关
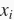 的导数。
的导数。
11.2.2.4. 梯度
假设函数
 的输入是一个
的输入是一个
 维向量
维向量
 ,输出是标量。函数
,输出是标量。函数
 有关
有关
 的梯度是一个由
的梯度是一个由
 个偏导数组成的向量:
个偏导数组成的向量:

为表示简洁,我们有时用
 代替
代替
 。
。
假设
 是一个向量,常见的梯度演算包括
是一个向量,常见的梯度演算包括

类似地,假设
 是一个矩阵,那么
是一个矩阵,那么

11.2.2.5. 海森矩阵
假设函数
 的输入是一个
的输入是一个
 维向量
维向量
 ,输出是标量。假定函数
,输出是标量。假定函数
 所有的二阶偏导数都存在,
所有的二阶偏导数都存在,
 的海森矩阵
的海森矩阵
 是一个
是一个
 行
行
 列的矩阵:
列的矩阵:

其中二阶偏导数

11.2.3. 概率
最后,我们简要介绍条件概率、期望和均匀分布。
11.2.3.1. 条件概率
假设事件
 和事件
和事件
 的概率分别为
的概率分别为
 和
和
 ,两个事件同时发生的概率记作
,两个事件同时发生的概率记作
 或
或
 。给定事件
。给定事件
 ,事件
,事件
 的条件概率
的条件概率

也就是说,

当满足

时,事件
 和事件
和事件
 相互独立。
相互独立。
11.2.3.2. 期望
离散的随机变量
 的期望(或平均值)为
的期望(或平均值)为

11.2.3.3. 均匀分布
假设随机变量
 服从
服从
 上的均匀分布,即
上的均匀分布,即
 。随机变量
。随机变量
 取
取
 和
和
 之间任意一个数的概率相等。
之间任意一个数的概率相等。
11.2.4. 小结
- 本节总结了本书中涉及的有关线性代数、微分和概率的基础知识。
11.2.5. 练习
- 求函数
 的梯度。
的梯度。
