3.2. 线性回归的从零开始实现

在了解了线性回归的背景知识之后，现在我们可以动手实现它了。尽管强大的深度学习框架可以减少大量重复性工作，但若过于依赖它提供的便利，会导致我们很难深入理解深度学习是如何工作的。因此，本节将介绍如何只利用NDArray和autograd来实现一个线性回归的训练。

首先，导入本节中实验所需的包或模块，其中的matplotlib包可用于作图，且设置成嵌入显示。

In [1]:

%matplotlib inline
from IPython import display
from matplotlib import pyplot as plt
from mxnet import autograd, nd
import random

3.2.1. 生成数据集

我们构造一个简单的人工训练数据集，它可以使我们能够直观比较学到的参数和真实的模型参数的区别。设训练数据集样本数为1000，输入个数（特征数）为2。给定随机生成的批量样本特征

，我们使用线性回归模型真实权重 和偏差 ，以及一个随机噪声项 来生成标签

其中噪声项

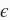服从均值为0、标准差为0.01的正态分布。噪声代表了数据集中无意义的干扰。下面，让我们生成数据集。

In [2]:

num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)

注意，features的每一行是一个长度为2的向量，而labels的每一行是一个长度为1的向量（标量）。

In [3]:

features[0], labels[0]

Out[3]:

(
 [2.2122064 0.7740038]
 <NDArray 2 @cpu(0)>,
 [6.000587]
 <NDArray 1 @cpu(0)>)

通过生成第二个特征features[:, 1]和标签 labels的散点图，可以更直观地观察两者间的线性关系。

In [4]:

def use_svg_display():
    # 用矢量图显示
    display.set_matplotlib_formats('svg')
 
def set_figsize(figsize=(3.5, 2.5)):
    use_svg_display()
    # 设置图的尺寸
    plt.rcParams['figure.figsize'] = figsize
 
set_figsize()
plt.scatter(features[:, 1].asnumpy(), labels.asnumpy(), 1);  # 加分号只显示图

我们将上面的plt作图函数以及use_svg_display函数和set_figsize函数定义在d2lzh包里。以后在作图时，我们将直接调用d2lzh.plt。由于plt在d2lzh包中是一个全局变量，我们在作图前只需要调用d2lzh.set_figsize()即可打印矢量图并设置图的尺寸。

3.2.2. 读取数据

在训练模型的时候，我们需要遍历数据集并不断读取小批量数据样本。这里我们定义一个函数：它每次返回batch_size（批量大小）个随机样本的特征和标签。

In [5]:

# 本函数已保存在d2lzh包中方便以后使用
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)  # 样本的读取顺序是随机的
    for i in range(0, num_examples, batch_size):
        j = nd.array(indices[i: min(i + batch_size, num_examples)])
        yield features.take(j), labels.take(j)  # take函数根据索引返回对应元素

让我们读取第一个小批量数据样本并打印。每个批量的特征形状为(10,2)，分别对应批量大小和输入个数；标签形状为批量大小。

In [6]:

batch_size = 10
 
for X, y in data_iter(batch_size, features, labels):
    print(X, y)
    break

[[ 0.1037775  -0.09160773]
 [-0.8720539   0.6916261 ]
 [ 2.0719576   0.29137844]
 [ 0.98115885  0.51506495]
 [-1.0267551   0.82085365]
 [-2.5899131  -0.3166397 ]
 [-0.22001728 -1.617725  ]
 [ 0.3088816   0.74587804]
 [-0.68202806  0.3181509 ]
 [-0.1461925  -0.3182019 ]]
<NDArray 10x2 @cpu(0)>
[ 4.728806    0.09408624  7.352827    4.40581    -0.65667355  0.10322509
  9.249024    2.2689395   1.7428185   4.9912653 ]
<NDArray 10 @cpu(0)>

3.2.3. 初始化模型参数

我们将权重初始化成均值为0、标准差为0.01的正态随机数，偏差则初始化成0。

In [7]:

w = nd.random.normal(scale=0.01, shape=(num_inputs, 1))
b = nd.zeros(shape=(1,))

之后的模型训练中，需要对这些参数求梯度来迭代参数的值，因此我们需要创建它们的梯度。

In [8]:

w.attach_grad()
b.attach_grad()

3.2.4. 定义模型

下面是线性回归的矢量计算表达式的实现。我们使用dot函数做矩阵乘法。

In [9]:

def linreg(X, w, b):  # 本函数已保存在d2lzh包中方便以后使用
    return nd.dot(X, w) + b

3.2.5. 定义损失函数

我们使用上一节描述的平方损失来定义线性回归的损失函数。在实现中，我们需要把真实值y变形成预测值y_hat的形状。以下函数返回的结果也将和y_hat的形状相同。

In [10]:

def squared_loss(y_hat, y):  # 本函数已保存在d2lzh包中方便以后使用
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

3.2.6. 定义优化算法

以下的sgd函数实现了上一节中介绍的小批量随机梯度下降算法。它通过不断迭代模型参数来优化损失函数。这里自动求梯度模块计算得来的梯度是一个批量样本的梯度和。我们将它除以批量大小来得到平均值。

In [11]:

def sgd(params, lr, batch_size):  # 本函数已保存在d2lzh包中方便以后使用
    for param in params:
        param[:] = param - lr * param.grad / batch_size

3.2.7. 训练模型

在训练中，我们将多次迭代模型参数。在每次迭代中，我们根据当前读取的小批量数据样本（特征X和标签y），通过调用反向函数backward计算小批量随机梯度，并调用优化算法sgd迭代模型参数。由于我们之前设批量大小batch_size为10，每个小批量的损失l的形状为(10,1)。回忆一下“自动求梯度”一节。由于变量l并不是一个标量，运行l.backward()将对l中元素求和得到新的变量，再求该变量有关模型参数的梯度。

在一个迭代周期（epoch）中，我们将完整遍历一遍data_iter函数，并对训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设3和0.03。在实践中，大多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得越大模型可能越有效，但是训练时间可能过长。而有关学习率对模型的影响，我们会在后面“优化算法”一章中详细介绍。

In [12]:

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
 
for epoch in range(num_epochs):  # 训练模型一共需要num_epochs个迭代周期
    # 在每一个迭代周期中，会使用训练数据集中所有样本一次（假设样本数能够被批量大小整除）。X
    # 和y分别是小批量样本的特征和标签
    for X, y in data_iter(batch_size, features, labels):
        with autograd.record():
            l = loss(net(X, w, b), y)  # l是有关小批量X和y的损失
        l.backward()  # 小批量的损失对模型参数求梯度
        sgd([w, b], lr, batch_size)  # 使用小批量随机梯度下降迭代模型参数
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().asnumpy()))

epoch 1, loss 0.040656
epoch 2, loss 0.000162
epoch 3, loss 0.000050

训练完成后，我们可以比较学到的参数和用来生成训练集的真实参数。它们应该很接近。

In [13]:

true_w, w

Out[13]:

([2, -3.4],
 [[ 1.9995768]
  [-3.3997586]]
 <NDArray 2x1 @cpu(0)>)

In [14]:

true_b, b

Out[14]:

(4.2,
 [4.199486]
 <NDArray 1 @cpu(0)>)

3.2.8. 小结

• 可以看出，仅使用NDArray和autograd模块就可以很容易地实现一个模型。接下来，本书会在此基础上描述更多深度学习模型，并介绍怎样使用更简洁的代码（见下一节）来实现它们。

3.2.9. 练习

• 为什么squared_loss函数中需要使用reshape函数？
• 尝试使用不同的学习率，观察损失函数值的下降快慢。
• 如果样本个数不能被批量大小整除，data_iter函数的行为会有什么变化？