姿态的数学表示方法

作者：nieyong

姿态有多种数学表示方式，常见的是四元数，欧拉角，矩阵和轴角。他们各自有其自身的优点，在不同的领域使用不同的表示方式。在四轴飞行器中使用到了四元数和欧拉角。

四元数

四元数是由爱尔兰数学家威廉·卢云·哈密顿在1843年发现的数学概念。从明确地角度而言，四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话，四元数就代表着一个四维空间，相对于复数为二维空间。

四元数大量用于电脑绘图（及相关的图像分析）上表示三维物件的旋转及方位。四元数亦见于控制论、信号处理、姿态控制、物理和轨道力学，都是用来表示旋转和方位。

相对于另几种旋转表示法（矩阵，欧拉角，轴角），四元数具有某些方面的优势，如速度更快、提供平滑插值、有效避免万向锁问题、存储空间较小等等。

以上部分摘自维基百科-四元数。

欧拉角

莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现。参考系又称为实验室参考系，是静止不动的。而坐标系则固定于刚体，随着刚体的旋转而旋转。

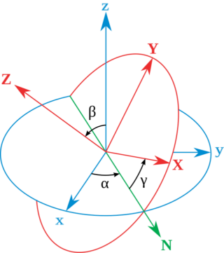
以上部分摘自维基百科-欧拉角。下面我们通过图例来看看欧拉角是如何产生的，并且分别对应哪个角度。

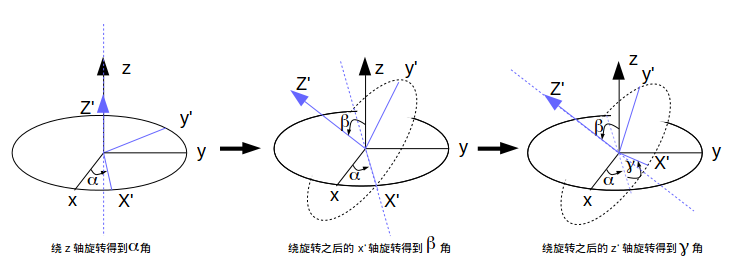
姿态解算为什么要用四元数和欧拉角

姿态解算的核心在于旋转，一般旋转有4种表示方式：矩阵表示、欧拉角表示、轴角表示和四元数表示。矩阵表示适合变换向量，欧拉角最直观，轴角表示则适合几何推导，而在组合旋转方面，四元数表示最佳。因为姿态解算需要频繁组合旋转和用旋转变换向量，所以采用四元数保存组合姿态、辅以矩阵来变换向量的方案。

总结来说，在crazepony中，姿态解算中使用四元数来保存飞行器的姿态，包括旋转和方位。在获得四元数之后，会将其转化为欧拉角，然后输入到姿态控制算法中。

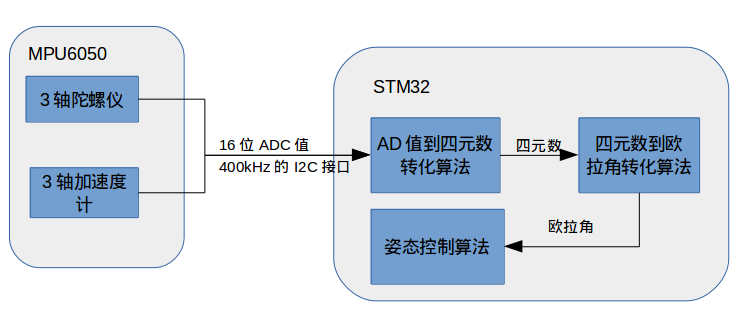
姿态控制算法的输入参数必须要是欧拉角。AD值是指MPU6050的陀螺仪和加速度值，3个维度的陀螺仪值和3个维度的加速度值，每个值为16位精度。AD值必须先转化为四元数，然后通过四元数转化为欧拉角。这个四元数可能是软解，主控芯片（STM32）读取到AD值，用软件从AD值算得，也可能是通过MPU6050中的DMP硬解，主控芯片（STM32）直接读取到四元数。具体参考《MPU60x0的四元数生成方式介绍》。

下面就是四元数软解过程，可以由下面这个框图表示：

扩展阅读-四元数的运算

下面介绍一下四元数，然后给出几种旋转表示的转换。这些运算在crazepony的代码中都会遇到。

四元数可以理解为一个实数和一个向量的组合，也可以理解为四维的向量。这里用一个圈表示q是一个四元数（很可能不是规范的表示方式）。

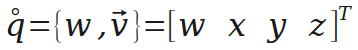
四元数的长度（模）与普通向量相似。

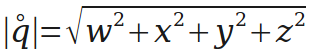
下面是对四元数的单位化，单位化的四元数可以表示一个旋转。

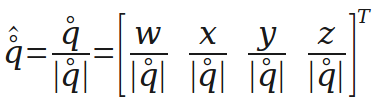
四元数相乘，旋转的组合就靠它了。

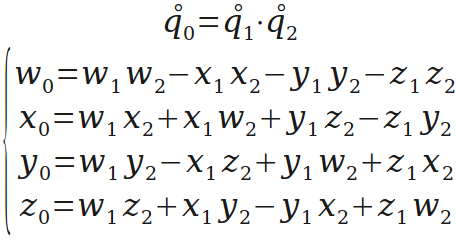
旋转的“轴角表示”转“四元数表示”。这里创造一个运算q(w,θ)，用于把绕单位向量w转θ角的旋转表示为四元数。

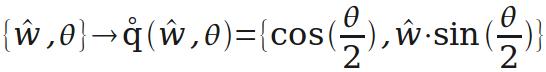
通过q(w,θ)，引伸出一个更方便的运算q(f,t)。有时需要把向量f的方向转到向量t的方向，这个运算就是生成表示对应旋转的四元数的（后面会用到）。

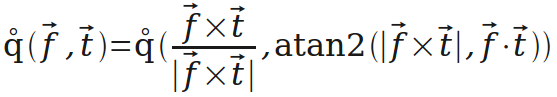
然后是“四元数表示”转“矩阵表示”。再次创造运算，用R(q)表示四元数q对应的矩阵（后面用到）。

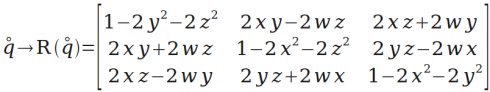
多个旋转的组合可以用四元数的乘法来实现。

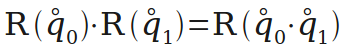
“四元数表示”转“欧拉角表示”。用于显示。