- 格子取数问题
- 题目描述
- 分析与解法
- 举一反三
格子取数问题
题目描述
有n*n个格子,每个格子里有正数或者0,从最左上角往最右下角走,只能向下和向右,一共走两次(即从左上角走到右下角走两趟),把所有经过的格子的数加起来,求最大值SUM,且两次如果经过同一个格子,则最后总和SUM中该格子的计数只加一次。
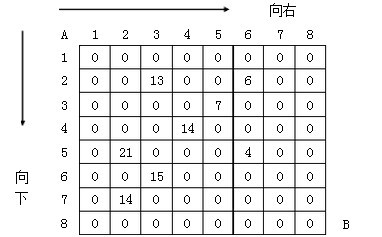
分析与解法
初看到此题,因为要让两次走下来的路径总和最大,读者可能最初想到的思路可能是让每一次的路径都是最优的,即不顾全局,只看局部,让第一次和第二次的路径都是最优。
但问题马上就来了,虽然这一算法保证了连续的两次走法都是最优的,但却不能保证总体最优,相应的反例也不难给出,请看下图:
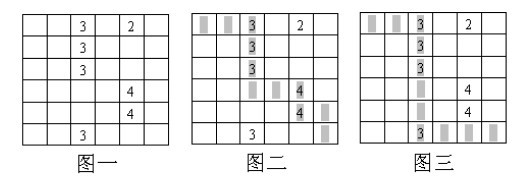
上图中,图一是原始图,那么我们有以下两种走法可供我们选择:
- 如果按照上面的局部贪优走法,那么第一次势必会如图二那样走,导致的结果是第二次要么取到2,要么取到3,
- 但若不按照上面的局部贪优走法,那么第一次可以如图三那样走,从而第二次走的时候能取到2 4 4,很显然,这种走法求得的最终SUM值更大;
为了便于读者理解,我把上面的走法在图二中标记出来,而把应该正确的走法在上图三中标示出来,如下图所示:
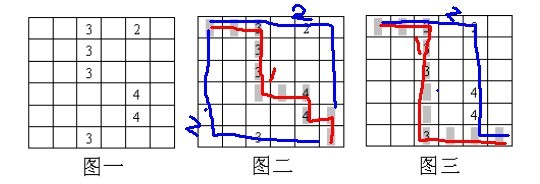
也就是说,上面图二中的走法太追求每一次最优,所以第一次最优,导致第二次将是很差;而图三第一次虽然不是最优,但保证了第二次不差,所以图三的结果优于图二。由此可知不要只顾局部而贪图一时最优,而丧失了全局最优。
局部贪优不行,我们可以考虑穷举,但最终将导致复杂度过高,所以咱们得另寻良策。
为了方便讨论,我们先对矩阵做一个编号,且以5*5的矩阵为例(给这个矩阵起个名字叫M1):
M1
0 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
从左上(0)走到右下(8)共需要走8步(2*5-2)。我们设所走的步数为s。因为限定了只能向右和向下走,因此无论如何走,经过8步后(s = 8)都将走到右下。而DP的状态也是依据所走的步数来记录的。
再来分析一下经过其他s步后所处的位置,根据上面的讨论,可以知道:
- 经过8步后,一定处于右下角(8);
- 那么经过5步后(s = 5),肯定会处于编号为5的位置;
- 3步后肯定处于编号为3的位置;
- s = 4的时候,处于编号为4的位置,此时对于方格中,共有5(相当于n)个不同的位置,也是所有编号中最多的。
故推广来说,对于n*n的方格,总共需要走2n - 2步,且当s = n - 1时,编号为n个,也是编号数最多的。
如果用DP[s,i,j]来记录2次所走的状态获得的最大值,其中s表示走s步,i和j分别表示在s步后第1趟走的位置和第2趟走的位置。
为了方便描述,再对矩阵做一个编号(给这个矩阵起个名字叫M2):
M2
0 0 0 0 0
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
4 4 4 4 4
把之前定的M1矩阵也再贴下:
M1
0 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
我们先看M1,在经过6步后,肯定处于M1中编号为6的位置。而M1中共有3个编号为6的,它们分别对应M2中的2 3 4。故对于M2来说,假设第1次经过6步走到了M2中的2,第2次经过6步走到了M2中的4,DP[s,i,j] 则对应 DP[6,2,4]。由于s = 2n - 2,0 <= i <= j <= n,所以这个DP共有O(n^3)个状态。
M1
0 1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
再来分析一下状态转移,以DP[6,2,3]为例(就是上面M1中加粗的部分),可以到达DP[6,2,3]的状态包括DP[5,1,2],DP[5,1,3],DP[5,2,2],DP[5,2,3]。
下面,我们就来看看这几个状态:DP[5,1,2],DP[5,1,3],DP[5,2,2],DP[5,2,3],用加粗表示位置DP[5,1,2] DP[5,1,3] DP[5,2,2] DP[5,2,3] (加红表示要达到的状态DP[6,2,3])
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5
2 3 4 5 6 2 3 4 5 6 2 3 4 5 6 2 3 4 5 6
3 4 5 6 7 3 4 5 6 7 3 4 5 6 7 3 4 5 6 7
4 5 6 7 8 4 5 6 7 8 4 5 6 7 8 4 5 6 7 8
因此:
DP[6,2,3] = Max(DP[5,1,2] ,DP[5,1,3],DP[5,2,2],DP[5,2,3]) + 6,2和6,3格子中对应的数值 (式一)
上面(式一)所示的这个递推看起来没有涉及:“如果两次经过同一个格子,那么该数只加一次的这个条件”,讨论这个条件需要换一个例子,以DP[6,2,2]为例:DP[6,2,2]可以由DP[5,1,1],DP[5,1,2],DP[5,2,2]到达,但由于i = j,也就是2次走到同一个格子,那么数值只能加1次。
所以当i = j时,
DP[6,2,2] = Max(DP[5,1,1],DP[5,1,2],DP[5,2,2]) + 6,2格子中对应的数值 (式二)
故,综合上述的(式一),(式二)最后的递推式就是
if(i != j)
DP[s, i ,j] = Max(DP[s - 1, i - 1, j - 1], DP[s - 1, i - 1, j], DP[s - 1, i, j - 1], DP[s - 1, i, j]) + W[s,i] + W[s,j]
else
DP[s, i ,j] = Max(DP[s - 1, i - 1, j - 1], DP[s - 1, i - 1, j], DP[s - 1, i, j]) + W[s,i]
其中W[s,i]表示经过s步后,处于i位置,位置i对应的方格中的数字。下一节我们将根据上述DP方程编码实现。
为了便于实现,我们认为所有不能达到的状态的得分都是负无穷,参考代码如下:
//copyright@caopengcs 2013const int N = 202;const int inf = 1000000000; //无穷大int dp[N * 2][N][N];bool IsValid(int step, int x1, int x2, int n) //判断状态是否合法{int y1 = step - x1, y2 = step - x2;return ((x1 >= 0) && (x1 < n) && (x2 >= 0) && (x2 < n) && (y1 >= 0) && (y1 < n) && (y2 >= 0) && (y2 < n));}int GetValue(int step, int x1, int x2, int n) //处理越界 不存在的位置 给负无穷的值{return IsValid(step, x1, x2, n) ? dp[step][x1][x2] : (-inf);}//状态表示dp[step][i][j] 并且i <= j, 第step步 两个人分别在第i行和第j行的最大得分 时间复杂度O(n^3) 空间复杂度O(n^3)int MinPathSum(int a[N][N], int n){int P = n * 2 - 2; //最终的步数int i, j, step;//不能到达的位置 设置为负无穷大for (i = 0; i < n; ++i){for (j = i; j < n; ++j){dp[0][i][j] = -inf;}}dp[0][0][0] = a[0][0];for (step = 1; step <= P; ++step){for (i = 0; i < n; ++i){for (j = i; j < n; ++j){dp[step][i][j] = -inf;if (!IsValid(step, i, j, n)) //非法位置{continue;}//对于合法的位置进行dpif (i != j){dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i - 1, j - 1, n));dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i - 1, j, n));dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i, j - 1, n));dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i, j, n));dp[step][i][j] += a[i][step - i] + a[j][step - j]; //不在同一个格子,加两个数}else{dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i - 1, j - 1, n));dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i - 1, j, n));dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i, j, n));dp[step][i][j] += a[i][step - i]; // 在同一个格子里,只能加一次}}}}return dp[P][n - 1][n - 1];}
复杂度分析:状态转移最多需要统计4个变量的情况,看做是O(1)的,共有O(n^3)个状态,所以总的时间复杂度是O(n^3)的,且dp数组开了N^3大小,故其空间复杂度亦为O(n^3)。
事实上,空间上可以利用滚动数组优化,由于每一步的递推只跟上1步的情况有关,因此可以循环利用数组,将空间复杂度降为O(n^2)。
即我们在推算dp[step]的时候,只依靠它上一次的状态dp[step - 1],所以dp数组的第一维,我们只开到2就可以了。即step为奇数时,我们用dp[1][i][j]表示状态,step为偶数我们用dp[0][i][j]表示状态,这样我们只需要O(n^2)的空间,这就是滚动数组的方法。滚动数组写起来并不复杂,只需要对上面的代码稍作修改即可,感兴趣的读者可以自己写代码实现下。
举一反三
1、给定m*n的矩阵,每个位置是一个非负整数,从左上角开始,每次只能朝右和下走,走到右下角,但只走一次,求总和最小的路径。
提示:因为只走一次,所以相对来说比较简单,dp[0, 0]=a[0, 0],且dp[x, y] = min(dp[x-1, y] + a[x, y]dp[x, y-1] + a[x, y])。
2、给定m*n的矩阵,每个位置是一个整数,从左上角开始,每次只能朝右、上和下走,并且不允许两次进入同一个格子,走到右上角,最小和。
分析:@cpcs :我们按列dp,假设前一列的最优值已经算好了,一旦往右就回不去了。枚举我们从对固定的(y-1)列,我们已经算好了最优值,我们枚举行x,朝右走到(x,y),然后再从(x,y)朝上走到(x,0),再从(x,y)朝下走到(x,n-1),所有这些第y列的值,作为第y列的候选值,取最优。
实际上,我们枚举了进入第y列的位置和在最终停在第y列的位置。这样保证我们不重复经过一个格子,也能保证我们不会往“左”走。
